Question

У трикутнику ABC бісектриса AE = EС. знайдіть кути трикутника ABC якщо AC дорівнює 2АВ
Допоможіть будь ласка!!!!!

Answer 1

Ответ:

Углы треугольника АВС равны 90°, 60° и 30°.

Объяснение:

В треугольнике ABC биссектриса AE = EC. Найдите углы треугольника ABC, если AC равен 2АВ.

Дано: ΔАВС;

АЕ - биссектриса;

АЕ = ЕС; АС = 2АВ.

Найти: углы ΔАВС.

Решение:

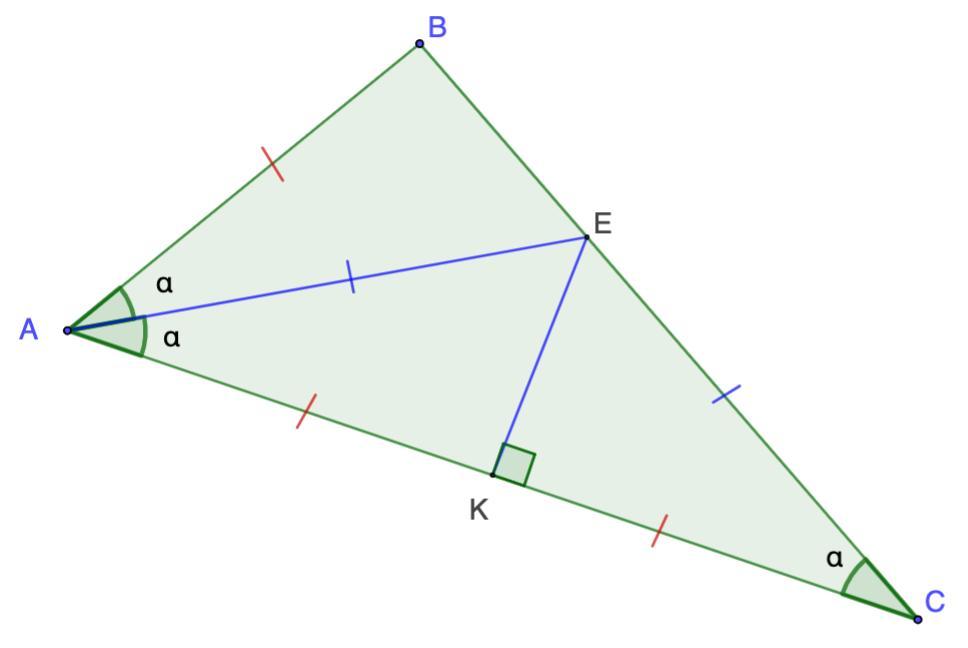
Отметим точку К - середину АВ, соединим К и Е.

Рассмотрим ΔАЕС - равнобедренный (АЕ = ЕС)

КЕ - медиана (построение)

• В равнобедренном треугольнике медиана, проведенная к основанию, является высотой.

⇒ ∠АКЕ = 90°.

Рассмотрим ΔАВЕ и ΔАКЕ.

АС = 2АВ   ⇒   АВ = АК

АЕ - общая, ∠ВАЕ = ∠КАЕ  (АЕ - биссектриса)

⇒ ΔАВЕ и ΔАКЕ (по 1 признаку)

⇒ ∠АКЕ = ∠АВЕ = 90° (как соответственные элементы)

ΔАВС - прямоугольный.

АС = 2АВ

• Если в прямоугольном треугольнике катет в два раза меньше гипотенузы, то он лежит против угла 30°.

⇒ ∠С = 30°

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠А = 90° - 30° = 60°

Углы треугольника АВС равны 90°, 60° и 30°.

#SPJ1