Question

3.Доведи, що при будь-яких значеннях a та b істинною є рівність:
Терміново!!!!
Даю 55 балів!!!

Answer 1

a) Розглянемо ліву частину рівняння: (ab)³ (a + b)³

Розкриємо кожну з скобок: (ab)³ (a + b)³ = a³b³(a + b)(a + b)(a + b)

Візьмемо a³b³ як один множник: a³b³(a + b)(a + b)(a + b) = a³b³(a + b)³

Тепер порівняємо отримане з правою частиною: -2b(3a² + b²)

Помножимо вираз у правій частині на a + b: -2b(3a² + b²) = -2b(3a² + b²)(a + b)

Розкриємо дужки: -2b(3a² + b²)(a + b) = -2b(3a³ + ab² + 3a²b + b³)

Тепер помножимо кожен член на ab³: -2b(3a³ + ab² + 3a²b + b³) = -2b(3a³b³ + a²b⁴ + 3a³b² + b⁴)

Виділимо спільні члени: -2b(3a³b³ + a²b⁴ + 3a³b² + b⁴) = -2b(a²b²(3ab + b²) + b²(3ab + b²))

Тепер можемо спростити вираз: -2b(a²b²(3ab + b²) + b²(3ab + b²)) = -2b(a²b² + b²)(3ab + b²)

Таким чином, ми дійсно отримали праву частину, і рівність справедлива.

б) Розглянемо ліву частину рівняння: (a+b)³ (a - b)³

Розкриємо кожну з скобок: (a+b)³ (a - b)³ = (a + b)(a + b)(a + b)(a - b)(a - b)(a - b)

Помножимо перші три скобки як один множник та наступні три як другий множник: (a + b)(a + b)(a + b)(a - b)(a - b)(a - b) = (a + b)³(a - b)³

Тепер порівняємо отримане з правою частиною: 2b(b² + 3a²)

Розкриємо дужки: 2b(b² + 3a²) = 2b(b² + 3a²)

Отже, ми дійсно отримали праву частину, і рівність справедлива.

Answer 2

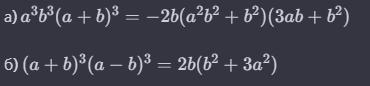
Розв'язок:

a)

$(a+b)^3=a^3+3a^2b+3ab^2+b^3\\(a-b)^3=a^3-3a^2b+3ab^2-b^3\\\\(a-b)^3-(a+b)^3=-2b(3a^2+b^2)\\a^3-3a^2b+3ab^2-b^3-(a^3+3a^2b+3ab^2+b^3)=-6a^2b-2b^3\\a^3-3a^2b+3ab^2-b^3-a^3-3a^2b-3ab^2-b^3=-6a^2b-2b^3\\-3a^2b+3ab^2-b^3-3a^2b-3ab^2-b^3=-6a^2b-2b^3\\-3a^2b-b^3-3a^2b-b^3=-6a^2b-2b^3\\-6a^2b-b^3-b^3=-6a^2b-2b^3\\-6a^2b-2b^3=-6a^2b-2b^3$

б)

$(a+b)^3=a^3+3a^2b+3ab^2+b^3\\(a-b)^3=a^3-3a^2b+3ab^2-b^3\\\\(a+b)^3-(a-b)^3=2b(b^2+3a^2)\\a^3+3a^2b+3ab^2+b^3-(a^3-3a^2b+3ab^2-b^3)=2b^3+6a^2b\\a^3+3a^2b+3ab^2+b^3-a^3+3a^2b-3ab^2+b^3=2b^3+6a^2b\\a^3+6a^2b+3ab^2+b^3-a^3-3ab^2+b^3=2b^3+6a^2b\\a^3+6a^2b+b^3-a^3+b^3=2b^3+6a^2b\\6a^2b+b^3+b^3=2b^3+6a^2b\\6a^2b+2b^3=2b^3+6a^2b\\2b^3+6a^2b=2b^3+6a^2b$