Question

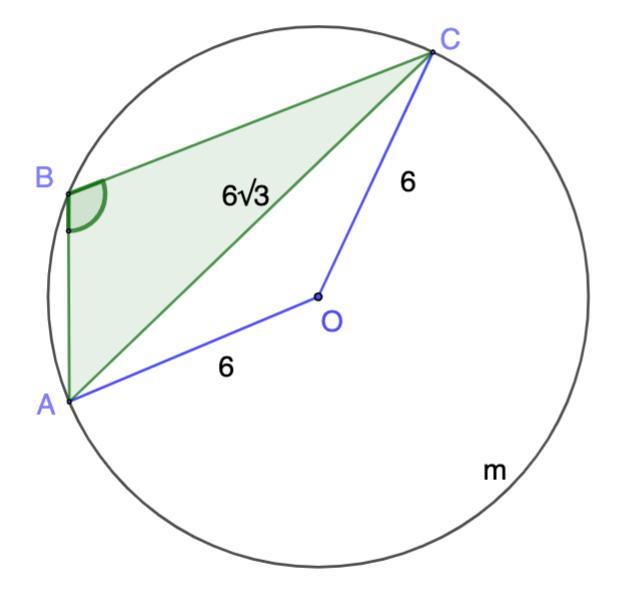
Известно, что радиус описанной окружности около треугольника равен 6, большая сторона этого треугольника равна 6√3. Чему равен угол, лежащий напротив этой стороны, если известно, что треугольник тупоугольный?

Answer 1

Ответ:

Угол, лежащий против большей стороны ΔАВС, равен 120°.

Объяснение:

Известно, что радиус описанной окружности около треугольника равен 6, большая сторона этого треугольника равна 6√3. Чему равен угол, лежащий напротив этой стороны, если известно, что треугольник тупоугольный?

Дано: ΔАВС - тупоугольный;

Окр.(О,R) - описанная около ΔАВС;

R = 6, AC = 6√3 - большая сторона.

Найти: ∠АВС

Решение:

1.

Рассмотрим ΔАОС - равнобедренный.

АО = ОС = R = 6

• Теорема косинусов: Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

АС² = АО² + ОС² - 2 · АО · ОС · cos∠AOC

108 = 36 + 36 - 2 · 6 · 6 · cos∠AOC

cos∠AOC = -36 : 72

cos∠AOC = -1/2   ⇒   ∠AOC = 120°

∠AOC - центральный угол.

• Центральный угол равен градусной мере дуги, на которую он опирается.

⇒ ◡АВС = 120°

• Градусная мера окружности равна 360°.

⇒ ◡AmC = 360° - 120° = 240°

∠ABC - вписанный.

• Вписанный угол измеряется половиной градусной меры дуги, на которую он опирается.

⇒ ∠АВС = 240° : 2 = 120°

2.

Или можно воспользоваться теоремой синусов:

• Отношение стороны треугольника к синусу противоположного угла равна удвоенному радиусу описанной окружности.

Из ΔАВС:

$\displaystyle \frac{AC}{sin\angle ABC}=2R\\ \\sin\angle ABC=\frac{AC}{2R}=\frac{6\sqrt{3} }{12}=\frac{\sqrt{3} }{2}$

По условию ΔАВС - тупоугольный

⇒ ∠ABC = 120°

#SPJ1