Предмет: Геометрия,
автор: StevePerry
Хелппппппппппппппппппппппппппппппппп
Приложения:
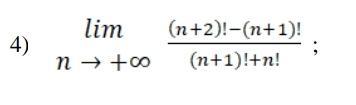
yugolovin:
А причем здесь геометрия?
если все сократить на n!, то от дроби останется ((n+1)(n+2)-(n+1))/(n+1+1)=(n+1)^2/(n+2), ну предел ее бесконечность
Ответы
Автор ответа:
1
Решение .
Найти предел .
Формула : .
Похожие вопросы
Предмет: Геометрия,
автор: zenakukik527
Предмет: Українська література,
автор: chernukhinl
Предмет: Українська мова,
автор: denysko90
Предмет: Литература,
автор: misskarakat00
Предмет: Литература,
автор: bogdanovaa001