Предмет: Алгебра,
автор: svecovaelizaveta72
Даны уравнения: 1) 3x²2 - 7x + 2 = 0; 2) 3x² + 5x+8 = 0. а) Определите, сколько корней имеет каждое уравнение. b) Найдите корни, если они существуют.
Приложения:

Ответы
Автор ответа:
0
Ааадааддадаөөөөәөіөөңөөғөңһңһіөіқіұіқіқңөөң уууууһ
Приложения:
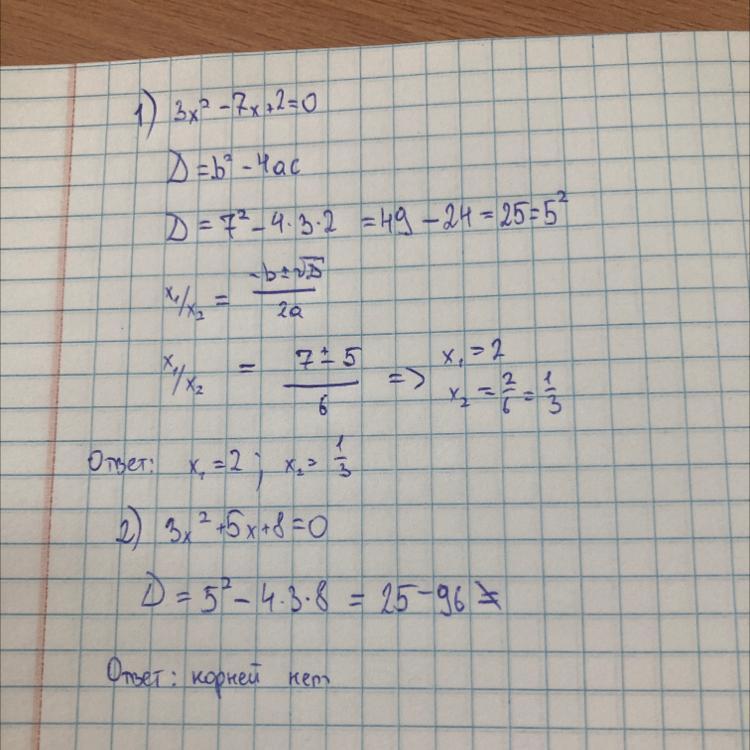
Автор ответа:
0
а) Для определения числа корней каждого уравнения, мы можем использовать дискриминант. Дискриминант вычисляется по формуле D = b²-4ac, где а, b и с - это коэффициенты перед x², x и свободный член соответственно.
1) Для уравнения 3x²-7x-6=0:
a = 3, b = -7, c = -6
D = (-7)² - 4 * 3 * (-6)
D = 49 + 72
D = 121
Так как дискриминант положительный и не равен нулю (D > 0), уравнение имеет два различных корня.
2) Для уравнения 2x²+x+16=0:
a = 2, b = 1, c = 16
D = (1)² - 4 * 2 * 16
D = 1 - 128
D = -127
Так как дискриминант отрицательный (D < 0), уравнение не имеет действительных корней.
б) Чтобы найти корни каждого уравнения, мы можем использовать формулу квадратного корня: x = (-b ± √D) / (2a).
1) Для уравнения 3x²-7x-6=0:
x₁ = (-(-7) + √121) / (2 * 3) = (7 + 11) / 6 = 18 / 6 = 3
x₂ = (-(-7) - √121) / (2 * 3) = (7 - 11) / 6 = -4 / 6 = -2/3
Таким образом, уравнение имеет два корня: x₁ = 3 и x₂ = -2/3.
2) Для уравнения 2x²+x+16=0:
Так как дискриминант отрицательный, уравнение не имеет действительных корней.
Таким образом, ответы на задачу:
а) 1) Уравнение 3x²-7x-6=0 имеет два корня.
2) Уравнение 2x²+x+16=0 не имеет действительных корней.
б) 1) Корни уравнения 3x²-7x-6=0: x₁ = 3 и x₂ = -2/3.
2) Уравнение 2x²+x+16=0 не имеет действительных корней.
1) Для уравнения 3x²-7x-6=0:
a = 3, b = -7, c = -6
D = (-7)² - 4 * 3 * (-6)
D = 49 + 72
D = 121
Так как дискриминант положительный и не равен нулю (D > 0), уравнение имеет два различных корня.
2) Для уравнения 2x²+x+16=0:
a = 2, b = 1, c = 16
D = (1)² - 4 * 2 * 16
D = 1 - 128
D = -127
Так как дискриминант отрицательный (D < 0), уравнение не имеет действительных корней.
б) Чтобы найти корни каждого уравнения, мы можем использовать формулу квадратного корня: x = (-b ± √D) / (2a).
1) Для уравнения 3x²-7x-6=0:
x₁ = (-(-7) + √121) / (2 * 3) = (7 + 11) / 6 = 18 / 6 = 3
x₂ = (-(-7) - √121) / (2 * 3) = (7 - 11) / 6 = -4 / 6 = -2/3
Таким образом, уравнение имеет два корня: x₁ = 3 и x₂ = -2/3.
2) Для уравнения 2x²+x+16=0:
Так как дискриминант отрицательный, уравнение не имеет действительных корней.
Таким образом, ответы на задачу:
а) 1) Уравнение 3x²-7x-6=0 имеет два корня.
2) Уравнение 2x²+x+16=0 не имеет действительных корней.
б) 1) Корни уравнения 3x²-7x-6=0: x₁ = 3 и x₂ = -2/3.
2) Уравнение 2x²+x+16=0 не имеет действительных корней.
Похожие вопросы
Предмет: Биология,
автор: shestiukeleonora
Предмет: География,
автор: lsidorenko495
Предмет: История,
автор: lop71010
Предмет: Алгебра,
автор: zakharskrebtsov
Предмет: Русский язык,
автор: bahahuahwv