Question

Сложная планиметрия.
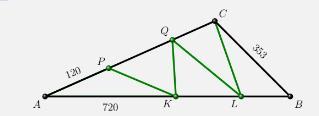
Дан треугольник ABC. На стороне AB этого треугольника выбраны точки K и L, а на стороне AC выбраны точки P и Q, как показано на рисунке. Оказалось, что ломаная PKQLC делит этот треугольник на 5 треугольников равной площади. Известно, что AP = 120, AK = 720, CB = 353. Найдите периметр треугольника ABC.

Answer 1

Ответ:

Периметр (несуществующего) треугольника ABC равен 2023.

Объяснение:

Воспользуемся одним из возможных способов решения этой задачи. Вспомним такую формулу для вычисления площади треугольника: половина произведения двух сторон треугольника и синуса угла между ними. Мы будем применять эту формулу для треугольников  APK, AQK, AQL, ACL, ACB. У всех указанных треугольников общий угол A, поэтому отношение их площадей будет равно отношению произведений прилежащих сторон.

Пусть AQ=a, AL=b, AC=c, AB=d. Имеем:

                      $\dfrac{S_{AQK}}{S_{APK}}=\dfrac{AQ\cdot AK}{AP\cdot AK}=\dfrac{a}{120}=2\Rightarrow a=240;$  

      $\dfrac{S_{AQL}}{S_{APK}}=\dfrac{ab}{120\cdot 720}=\dfrac{240b}{120\cdot 720}=\dfrac{b}{360}=3\Rightarrow b=3\cdot 360=1080;$

                    $\dfrac{S_{ACL}}{S_{APK}}=\dfrac{bc}{120\cdot 720}=\dfrac{3\cdot 360c}{120\cdot 720}=\dfrac{c}{80}=4\Rightarrow c=320;$

             $\dfrac{S_{ACB}}{S_{APK}}=\dfrac{320d}{120\cdot 720}=\dfrac{8d}{3\cdot 720}=\dfrac{d}{3\cdot 90}=5\Rightarrow d=1350.$

Поэтому периметр треугольника ABC равен

                      $c+d+353=320+1350+353=2023.$

Замечание. На самом деле треугольник со сторонами 320, 1350, 353 не существует, поскольку сумма двух его сторон меньше третьей:

320+353<1350.