Предмет: Алгебра,
автор: winboss275
Дано:А(3;5)
В(3;7)
С(7;5)
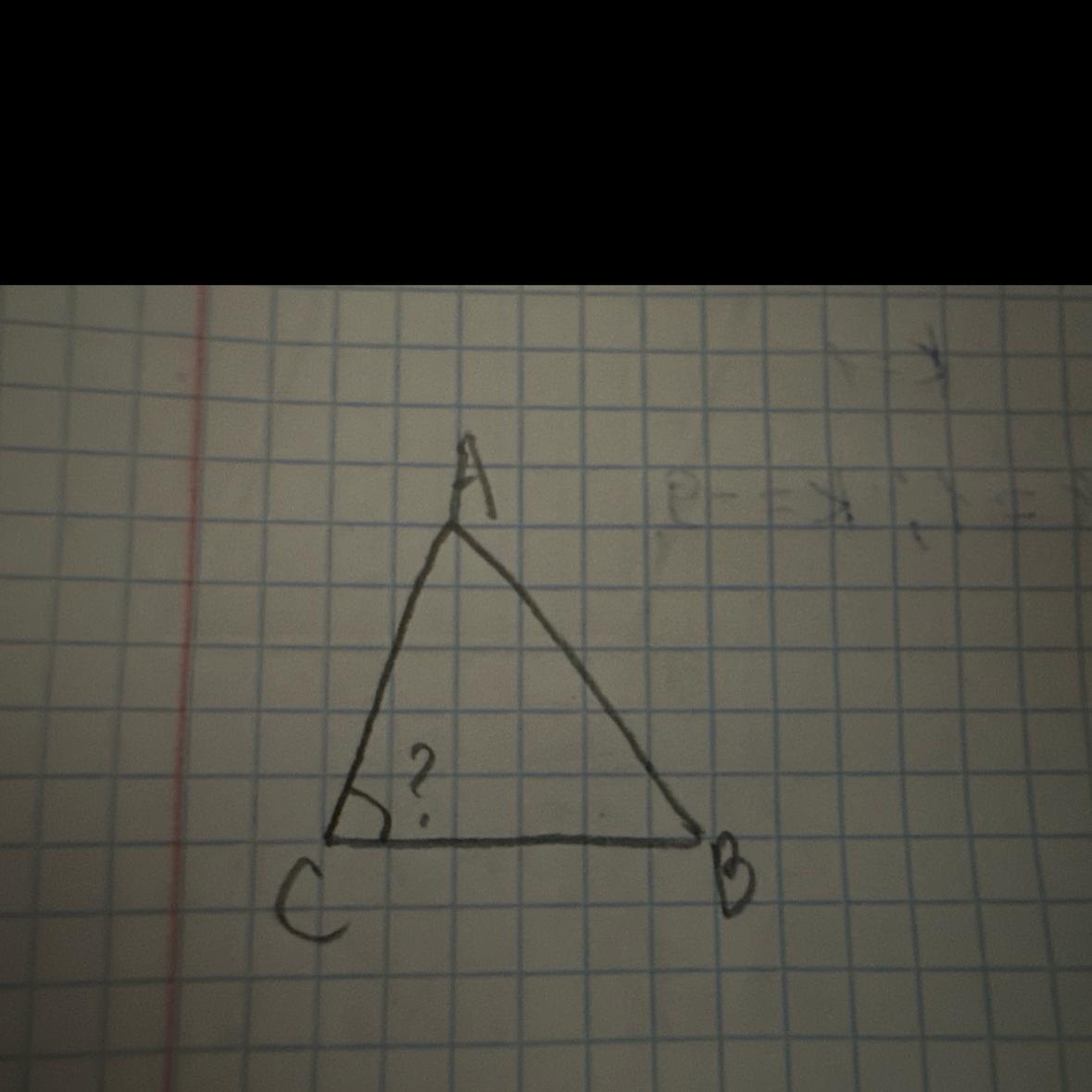
Знайти:<С
Приложения:
Ответы
Автор ответа:
1
Ответ:
Угол С можно найти как угол между векторами СА и СВ .
Приложения:

fctdgsygfdhngfxzgsac:
NNNLLL54, здравствуйте! спасибо большое что помогли с заданиями) если у Вас будет еще возможность помочь, то у меня в профиле есть несколько заданий)
Похожие вопросы
Предмет: Английский язык,
автор: yakonon
Предмет: МХК,
автор: adamutu38
Предмет: Українська мова,
автор: misugaoleksandr
Предмет: Алгебра,
автор: ds7924110
Предмет: Английский язык,
автор: zholdybekanizat