Question

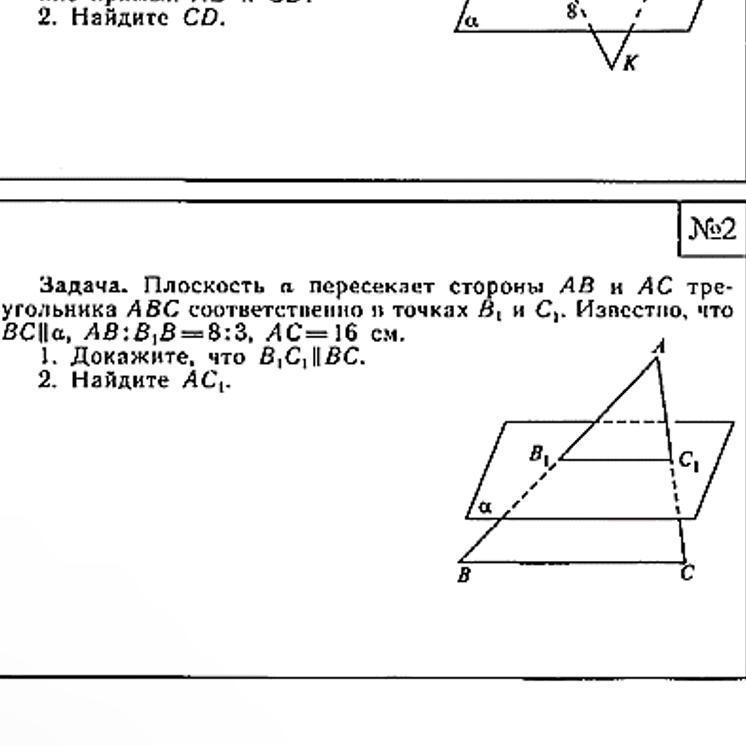
Задача. Плоскость а пересекает стороны АВ и АС треугольника АВС соответственно в точках В1 и С1. Известпо, что BC|lа, AB:B,B=8:3, AC=16 см.
1. Докажите, что В,C1IIBC.
2. Найдите АC1.

Answer 1

Ответ:

1. Для доказательства того, что B1C1 || BC, мы можем использовать теорему Талеса. Так как AB:ВB1 = 8:3, то мы можем предположить, что B1C1 || BC. Для доказательства этого, мы можем использовать теорему о параллельных линиях и углах, а также свойства подобных треугольников.

2. Чтобы найти AC1, мы можем воспользоваться теоремой Талеса. Так как AB:ВB1 = 8:3, то мы можем предположить, что B1C1 || BC. Теперь мы можем использовать теорему Талеса для нахождения AC1. Так как AC:СС1 = AB:ВB1, то мы можем записать:

AC:СС1 = 8:3

AC = (8/3) * CC1

AC = (8/3) * 16

AC = 42.7 см

Таким образом, длина отрезка AC1 равна 42.7 см.