Предмет: Алгебра,
автор: naste4ka38
7. Довести, що значення виразу залежить відзначеної.
Приложения:
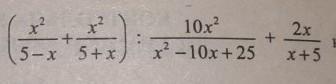
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Химия,
автор: lizka2310lizka
Предмет: Українська література,
автор: nikaluka280710
Предмет: Алгебра,
автор: tikidok30
Предмет: Математика,
автор: hikkanov538