Предмет: Геометрия,
автор: pensilvania13
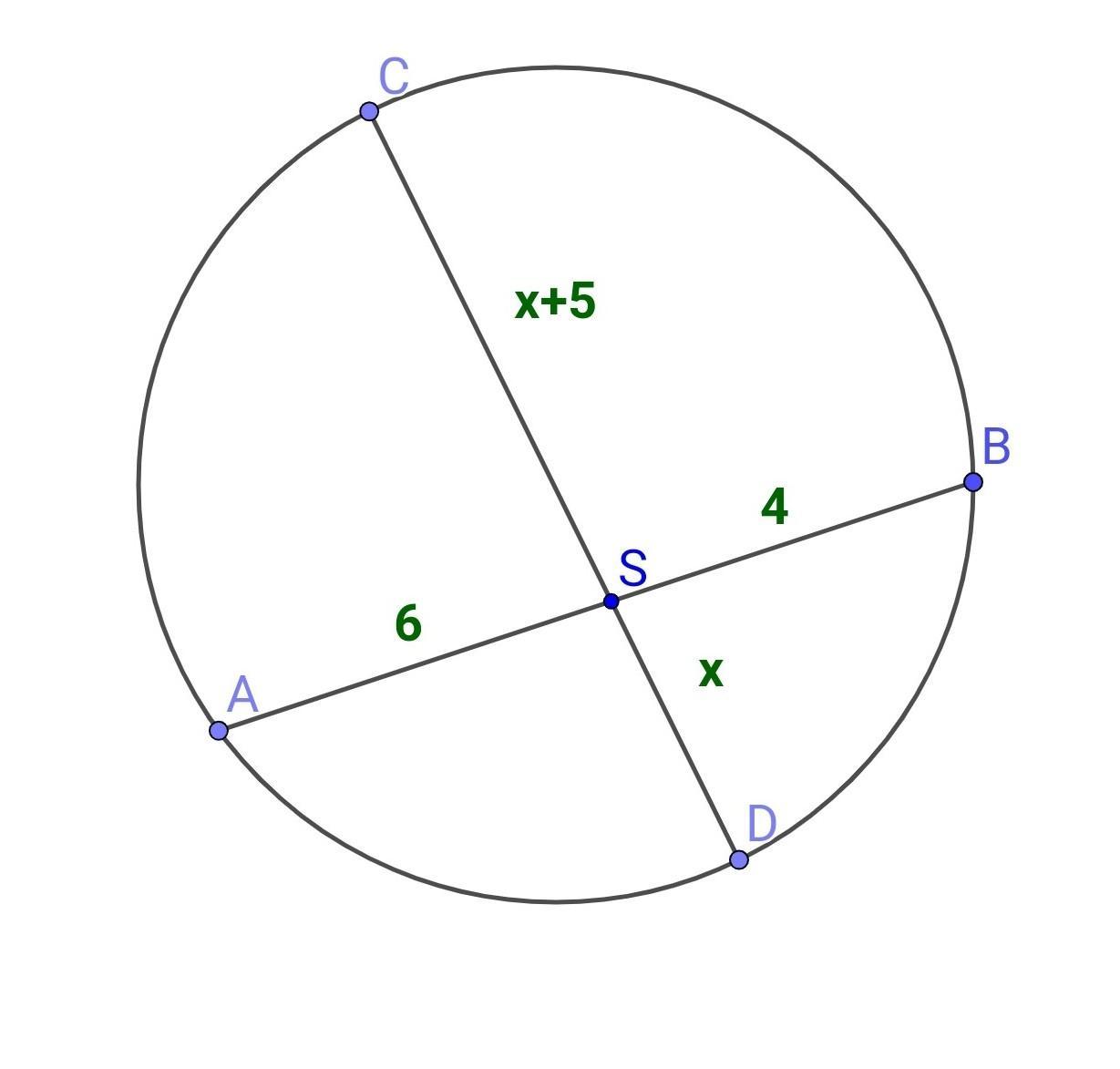
при пересечении двух хорд одна из них делится на отрезки 6 см и 4 см а вторая на отрезки один из которых меньше другого на 5 см найди длину второй хорды
Ответы
Автор ответа:
3
Ответ:
Длина второй хорды равна 11 см
Объяснение:
При пересечении двух хорд одна из них делится на отрезки 6 см и 4 см, а вторая на отрезки один из которых меньше другого на 5 см. Найди длину второй хорды.
- Если хорды AB и CD пересекаются в точке S, то AS • SB = CS • SD
РЕШЕНИЕ
Известно хорды AB и CD пересекаются в точке S. AS = 6 см, SB = 4 см.
Пусть SD = х, тогда SС = (х +5).
Тогда по свойству хорд, что пересекаются :
AS • SB = CS • SD
6 • 4 = х • (х +5)
х² + 5х - 24 = 0
D = b² - 4ac = 5² - 4 •(-24) = 25 + 96 = 121 = 11²
х₂<0, поэтому не является решением.
Тогда SD = 3 (см), а SC = 3 + 5 = 8 (см).
Найдём хорду CD:
CD = CS + SD = 3 + 8 = 11 (см)
ОТВЕТ: 11 см
#SPJ1
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: mega34911
Предмет: Математика,
автор: Leonardo20121984
Предмет: Английский язык,
автор: Kayirhzan
Предмет: Қазақ тiлi,
автор: musaevasahinur
Предмет: Математика,
автор: GrechkaShow