Предмет: Алгебра,
автор: theawekencat5556
Побудуйте графік функції і з'ясуйте, при
яких значеннях аргументу функція у = -x² - 2х + 3 набуває додатнiх значень?
(ІЗ ПОВНИМ РОЗВʼЯЗАННЯМ!)
Ответы
Автор ответа:
1
Ответ:
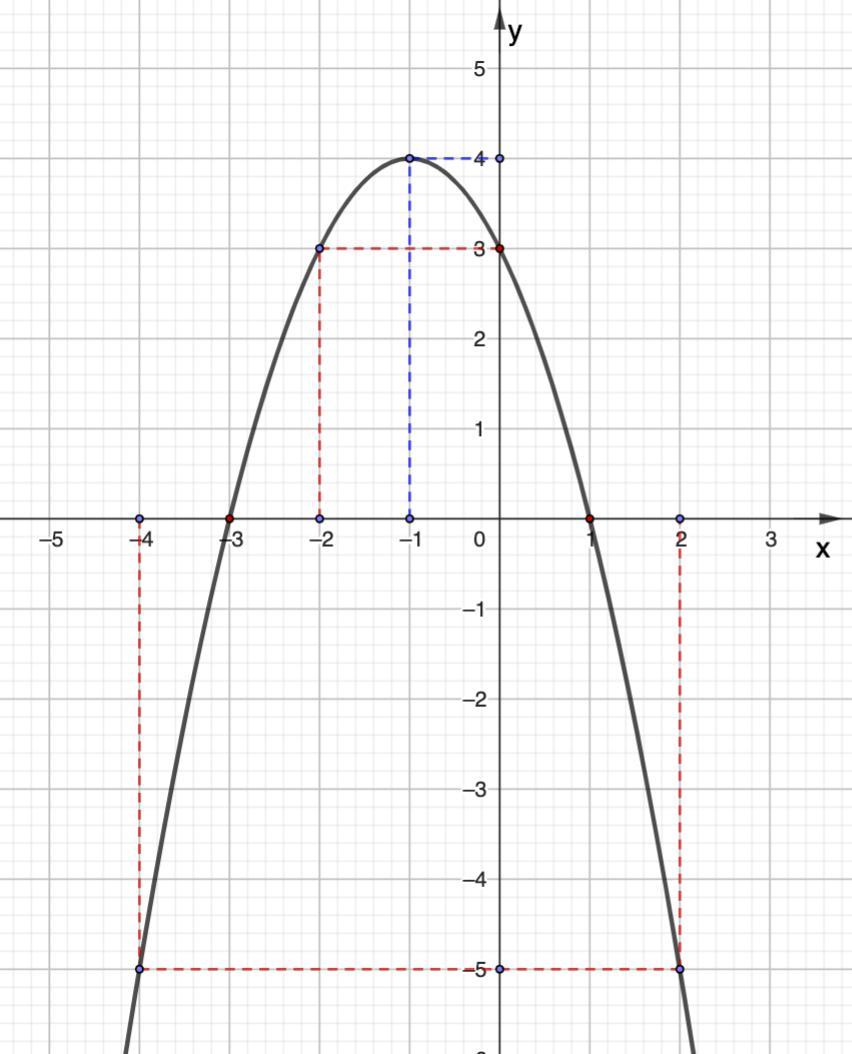
График построен.
Положительное значение функция приобретает при х ∈ (-3; 1).
Объяснение:
Постройте график функции и выясните, при каких значениях аргумента функция у = - x² - 2х + 3 приобретает положительные значения?
у = - x² - 2х + 3
- квадратичная функция вида у = ax² + bx + c, график парабола, a < 0 ⇒ ветви вниз.
Вершина:
Координаты вершины (-1; 4)
х = -1 - ось симметрии.
Пересечение с осью Ох:
-х² - 2х + 3 = 0 |·(-1)
х² + 2x - 3 = 0
По теореме Виета:
х₁ = -3; х₂ = 1
Дополнительные точки:
Строим график.
Положительное значение функция приобретает при х ∈ (-3; 1).
#SPJ1
Приложения:
Похожие вопросы
Предмет: Литература,
автор: ilyagorchayev
Предмет: Українська мова,
автор: darunazaac2012
Предмет: География,
автор: zasfanchik
Предмет: Русский язык,
автор: Аноним