Предмет: Геометрия,
автор: diasmaripzanov204
3. (bn) - геометрическая прогрессия. bi =7, q= -2. Найдите четвертый член прогрессии. [2]
Приложения:
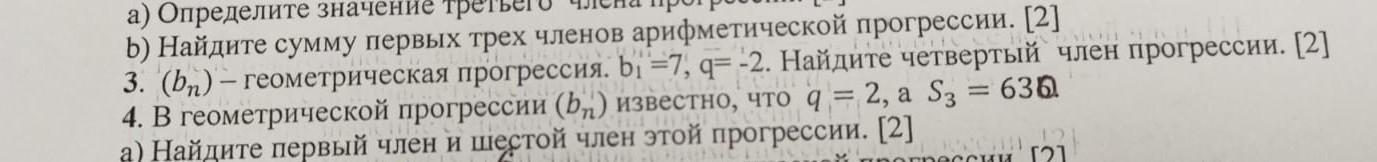
Ответы
Автор ответа:
1
Ответ:
Используем формулу n – ого члена геометрической прогрессии.
Так как геометрическая прогрессия задана формулой bn = 10 * 3n,
определим через нее третий, четвертый и пятый член прогрессии.
b3 = 10 * 33 10 * 27 = 270.
b4 = 10 * 34 10 * 81 = 810.
b5 = 10 * 35 10 * 243 = 2430.
Используем формулу n – ого члена геометрической прогрессии и выразим из нее знаменатель прогрессии
bn = b(n-1)/ * q.
q = bn / b(n-1) = b4 / b3 = 810 / 270 = 3.
Ответ: b3 = 270, b5 = 2430, q = 3.
Объяснение:
ну вот
diasmaripzanov204:
Спасибо
А как 270 получилось в начале
А как 270 получилось в начале ?
Похожие вопросы
Предмет: Химия,
автор: olshevskiy0310z
Предмет: Литература,
автор: hannaruzhylo
Предмет: Українська література,
автор: viccadetoy
Предмет: Геометрия,
автор: gitor22
Предмет: Геометрия,
автор: animesnikbest