Question

Визначити об'єм тіла, утвореного обертанням навколо осі ...... кола ......... .

Answer 1

Ответ:

$\displaystyle \frac{4}{3} \pi R^3$

Объяснение:

$\displaystyle V=\pi \int\limits^a_b {y^2(x)} \, dx$

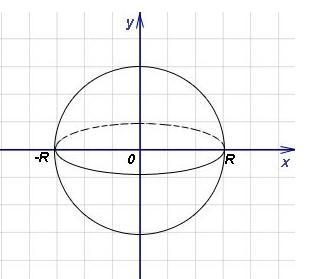
У нас получается тело, образованное  при вращении вокруг оси ОХ полукруга радиуса R с центром в начале координат. (попросту говоря, получается шар.)

Пределы интегрирования [-R; R]

y²(x) = R² - x²

$\displaystyle V=\pi \int\limits^{R}_{-R} {\bigg(R^2-x^2\bigg)} \, dx =\pi\bigg( \int\limits^{R}_{-R} {R^2} \, dx - \int\limits^{R}_{-R} {x^2} \, dx \bigg)=\\\\\\=\pi \bigg(R^2x\bigg|_{-R}^R-\frac{x^3}{3} \bigg|_{-R}^R\bigg)=\pi \bigg(R^2R-R^2(-R)\bigg)-\pi \bigg(\frac{R^3}{3} -(\frac{-R^3}{3} )\bigg)=\\\\\\=\pi \bigg(2R^3-\frac{2R^3}{3} \bigg)=\frac{4}{3} \pi R^3$

что есть известная нам формула объема шара.