Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Обчислити площу фігури, обмеженої кривими .......... , .......... та прямими ...... , ........ .
Приложения:

Ответы
Автор ответа:
1
Ответ:
Объяснение:
Формула для расчета
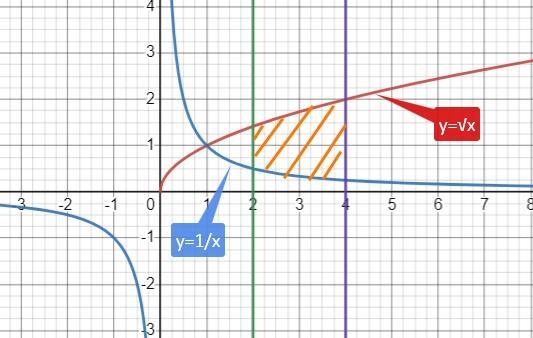
Прежде всего рисуем графики
По графикам определяем
(график лежит "выше" на координатной плоскости.)
пределы интегрирования от 2 до 4
Итак, пошли считать интеграл
Приложения:
fctdgsygfdhngfxzgsac:
спасибо большое))
пожалуйста -))
Похожие вопросы
Предмет: Русский язык,
автор: s88895217
Предмет: География,
автор: verxiws
Предмет: Математика,
автор: 17apanasenkooleksand
Предмет: Русский язык,
автор: segizbaevazanerke
Предмет: Литература,
автор: veneraburibaeva723