Решите пожалуйста подробно
Ответы
Ответ:
51.
Объяснение:
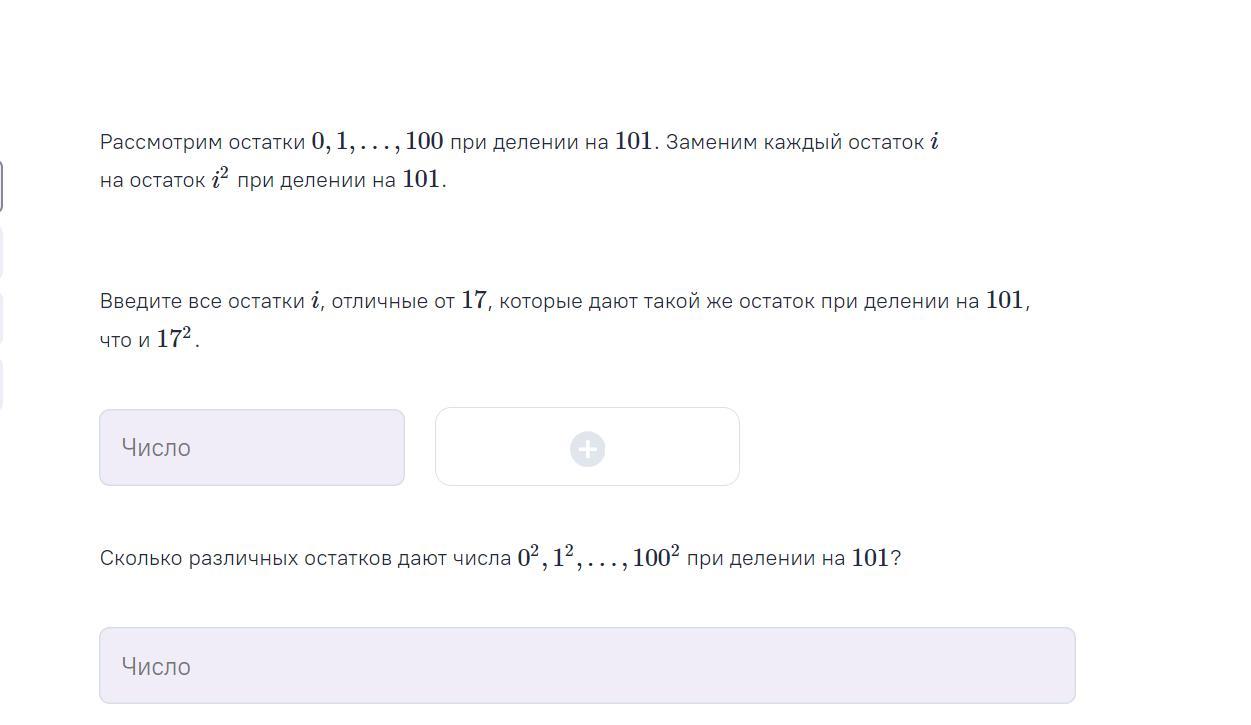
Первоначальное наблюдение: если целые числа i и j удовлетворяют условию i+j=101, то числа i² и j² дают одинаковые остатки при делении на 101. В самом деле,
i²-j²=(i-j)(i+j)=101(i-j),
что и означает равенство остатков (которые при вычитании "скушали" друг друга).
Посмотрим, каким условиям должны удовлетворять целые числа i и j, лежащие в промежутке от 0 до 100, чтобы числа i² и j² давали одинаковые остатки при делении на 101. Отметим сначала, что число 101 простое, то есть делится только на 1 и на себя.
Для определенности предположим, что i>j.
Пусть i² и j² дают одинаковые остатки при делении на 101. Это равносильно тому, что i²-j² делится на 101. Иными словами,
(i-j)(i+j)=101k.
Поскольку 0<i-j<101, а 101 простое число, j+j делится на 101.
А поскольку 0<i+j<200, делаем однозначный вывод, что i+j=101.
Итак, для различных целых чисел, взятых из промежутка от 0 до 100, условие
i+j=101
является необходимым и достаточным для того, чтобы квадраты этих чисел давали одинаковые остатки при делении на 101.
Иными словами, одинаковые остатки дают квадраты чисел 0 и 101 (ой, прошу прощения, 101 не входит в требуемый промежуток, так что 0 оказался без пары); 1 и 100; 2 и 99; 3 и 98; ...; 50 и 51. Всего 50 пар и одинокий ноль - получается 51 остаток.
Отдельный вопрос был про 17 - ладно, давайте посчитаем, сколько будет, если из 101 вычесть 17:
101-17=84.