Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Обчислити інтеграл частинами.
Приложения:
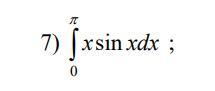
Ответы
Автор ответа:
1
Ответ:
Вычислить определённый интеграл .
Применяем формулу интегрирования по частям в определённом интеграле .
Приложения:
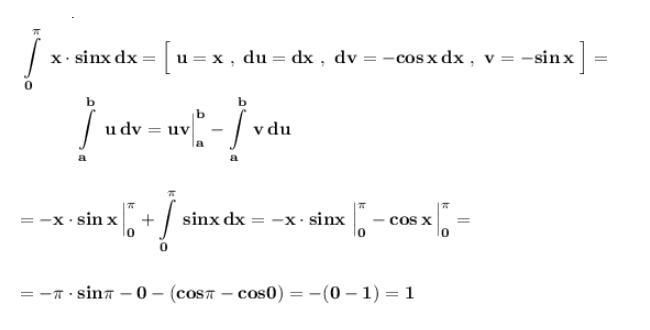
Похожие вопросы
Предмет: Українська мова,
автор: endruuspeh
Предмет: Українська література,
автор: aniki93
Предмет: Математика,
автор: natalagrab822
Предмет: Алгебра,
автор: dadoctor002
Предмет: Английский язык,
автор: rus4kovadaria4