Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Обчислити інтеграл заміною змінних.
Приложения:

Ответы
Автор ответа:
1
Ответ:
Вычислить определённый интеграл .
Применяем метод замены переменной в определённом интеграле .
Приложения:
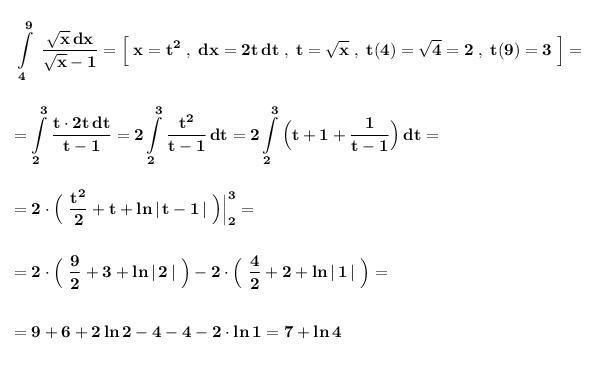
fctdgsygfdhngfxzgsac:
спасибо большое)
Похожие вопросы
Предмет: Физика,
автор: user463
Предмет: Українська мова,
автор: nikitop57
Предмет: Химия,
автор: xbow88848
Предмет: Обществознание,
автор: vikkvika
Предмет: Биология,
автор: svetamerkureva590