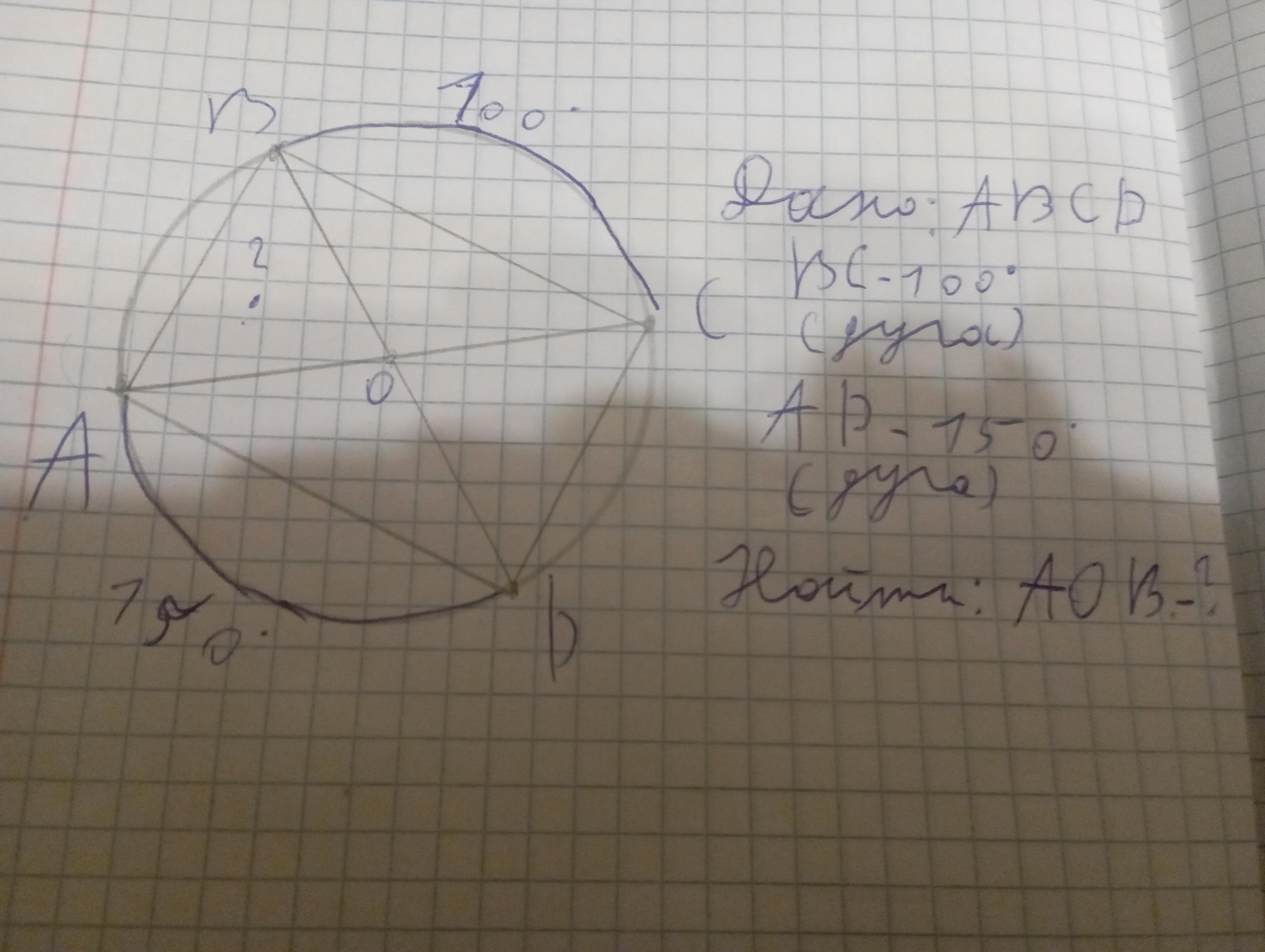
Дан вписанный в окружность произвольный четырехугольник ABCD. Проведены диагонали (центральный угол). Градусная мера дуги BC-100°, AD-150°. Найти градусную меру дуги AB (или же AOB).
Ответы
Ответ:
За властивостями вписаного чотирикутника, сума протилежних кутів, утворених діагоналями, дорівнює 180 градусів.
Отже, у центральному куті між дугами BC і AD ми можемо знайти градусну міру дуги AB.
Градусна міра дуги BC - 100°
Градусна міра дуги AD - 150°
Сума цих двох дуг дорівнює градусній мірі у центральному куті між ними:
Градусна міра у центральному куті = Градусна міра дуги BC + Градусна міра дуги AD = 100° + 150° = 250°
Але це ще не градусна міра дуги AB. Це градусна міра центрального кута між ними. А дуга AB - це половина цього центрального кута, оскільки вона є діагоналлю чотирикутника. Отже, щоб знайти градусну міру дуги AB (або AOB), потрібно поділити міру центрального кута між ними на 2:
Градусна міра дуги AB = Градусна міра у центральному куті / 2 = 250° / 2 = 125°
Отже, градусна міра дуги AB (або AOB) дорівнює 125°.