Question

У рівнобічну трапецію, більша основа
якої на 14 см більша за меншу основу,
вписано коло. Знайди периметр та
площу трапеції, якщо бічна сторона
дорівнює 25 см.

СРООООЧНОООО

Answer 1

Відповідь:

Р=100см

S=600см²

Пояснення:

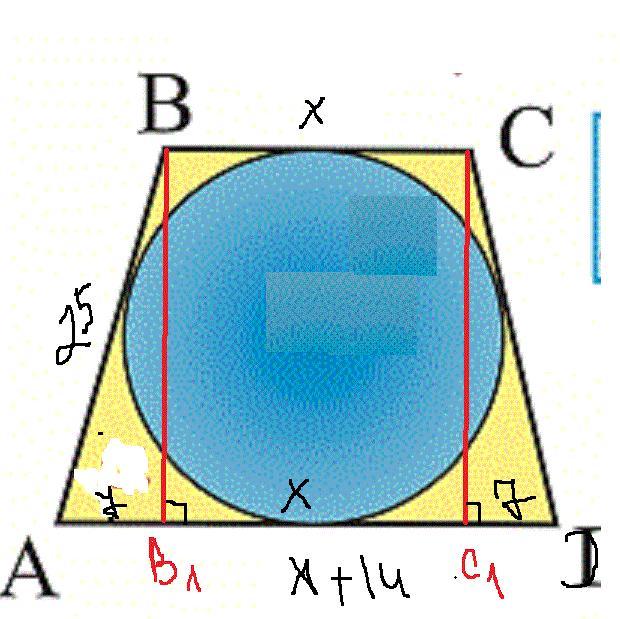
Якщо сума основ трапеції дорівнює сумі її бічних сторін, то в таку трапецію можна вписати коло.
Нехай менша основа трапеції х см, тоді більша (х+14)см.

х+х+14=25+25;

2х=50-14;

2х=36;
х=36:2;

х=18(см)

АД=х+14=18+14=32 (см)
Проведемо перпендикуляри ВВ₁ та СС₁ до АД.
В₁ВСС₁- прямокутник, ВС=В₁С₁  =18 см
АВ₁ =14:2=7 cм
Розглянемо ΔАВВ₁, де ∠В₁  =90°, за теор. Піфагора АВ²=ВВ₁²+АВ₁² →

$BB_{1}=\sqrt{AB^2-AB_{1}^2 } =\sqrt{25^2-7^2}=\sqrt{(25-7)(25+7)}=24$ (см)
$S=\frac{AD+BC}{2}*BB_{1}=\frac{18+32}{2}*24=50*12=600$(cм²)

Р=АВ+ВС+СД+АД=100 см