Предмет: Алгебра,
автор: lavrovskyi
Решить уравнения (желательно через ОДЗ), решение покороче
Алгебра 10 класс
Приложения:
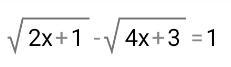
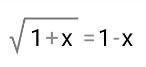
Ответы
Автор ответа:
0
Ответ:
1)
2)
Объяснение:
1)
ОДЗ
проверка
----------------------------
2)
ОДЗ
проверка
======================
1) 2-й способ
ОДЗ
Похожие вопросы
Предмет: Українська література,
автор: lihvaroman972
Предмет: Геометрия,
автор: nazarlimar018
Предмет: Українська мова,
автор: s4660937
Предмет: Литература,
автор: damirivanov1991
Предмет: Другие предметы,
автор: grishin8659