Предмет: Алгебра,
автор: yar41ks
Решите графически систему {(x-3)^2+(y-3)^2=9 {x-y=-3
Ответы
Автор ответа:
1
Ответ:
Объяснение:
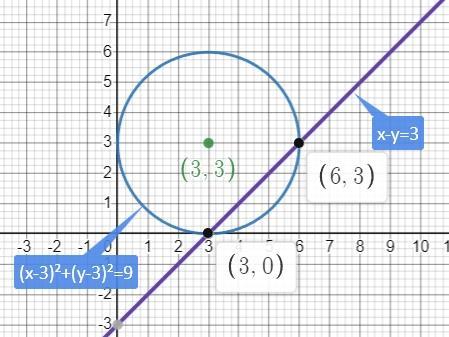
Строим график каждого уравнения по отдельности.
первое уравнение - уравнение окружности с центром в точке (3; 3) диаметром 3.
Второе уравнение - прямая у = х-3, строим по точкам
х = 0 у = -3
х = 1 у= -2
На координатной плоскости находим точки пересечения графиков (6; 3) и (3; 0) - это и есть решения системы
Приложения:
Похожие вопросы
Предмет: Немецкий язык,
автор: vitavinichenko
Предмет: Українська література,
автор: polivodaartem321
Предмет: Математика,
автор: husainova1997malika
Предмет: Литература,
автор: МаргаритаSV
Предмет: Физкультура и спорт,
автор: btslove13