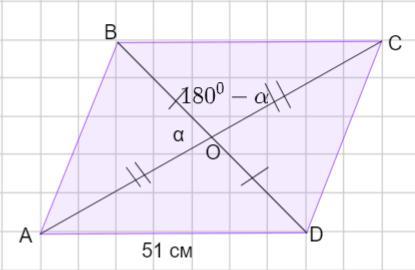
Діагоналі паралелограма дорівнюють 40 см і 74 см, а одна з його сторін - 51 см. Знайдіть площу паралелограма.
Ответы
Ответ:
1 224 cм²
Объяснение:
Диагонали параллелограмма равны40 см и 74 см, а одна из сторон 51 см. Найти площадь параллелограмма.
Пусть дан параллелограмм ABCD. Диагонали ВD= 40 см, АС =74 см. Сторона АD= 51 см.
АС ∩ ВD = О.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Тогда АО =ОС =74 : 2 =37 см;
ВО =ОD = 40 : 2 =20 см.
При пересечении диагоналей образовались четыре треугольника, площади которых равны .
Пусть ∠АОВ =α. Тогда смежный с ним ∠ВОС = 180° - α.
Так как выполняется равенство
sin ( 180° - α) =sin α, то если найти площади ΔАОВ и ΔВОС как полупроизведение сторон на синус угла между ними , получим , что площади треугольников равны.
Значит, можно найти площадь ΔАОD и умножить на 4.
Найдем площадь треугольника со сторонами 20 см, 37 см и 51 см по формуле Герона.
cм.
Тогда площадь найдем по формуле
см²
Площадь одного треугольника равна 306 см². Тогда найдем площадь параллелограмма
S = 306 · 4 = 1 224 cм²