Предмет: Математика,
автор: kotiklikol
Все подробно расписать. Вычислить площадь фигуры, которая ограничена данными линиями:
Приложения:
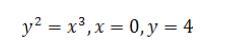
Ответы
Автор ответа:
0
Ответ:
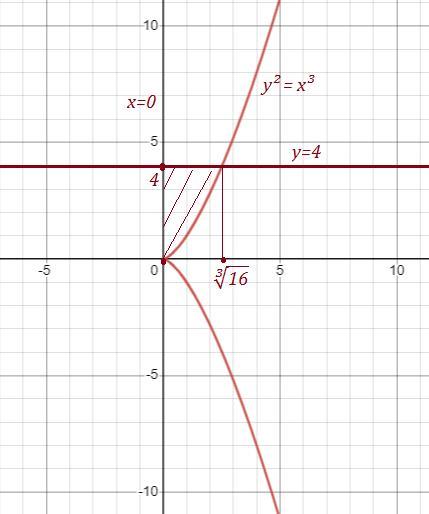
Область ограничена полукубической параболой у² = х³ , прямыми
х = 0 и у = 4 . Вычислить площадь области .
Точки пересечения :
Приложения:

mgricuk789:
Доброго ранку! Допоможіть, будь ласка, з алгеброю. Завдання в профілі.
Похожие вопросы
Предмет: Английский язык,
автор: Nikitapon1
Предмет: Русский язык,
автор: QqBCEM
Предмет: Другие предметы,
автор: zannabajburina
Предмет: Математика,
автор: Dumoooon
Предмет: Алгебра,
автор: banny764