Предмет: Алгебра,
автор: ThomasShelby21
Решите систему уравнений:
Приложения:
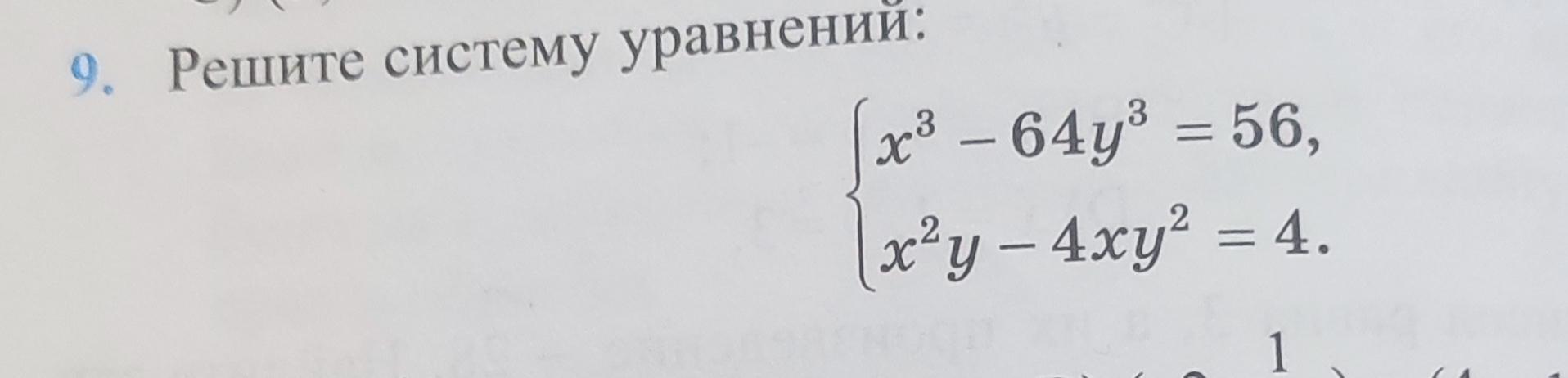
forqforq:
https://znanija.com/task/54258567
Ответы
Автор ответа:
0
Ответ:
или
Объяснение:
Умножим второе уравнение на 12 и получим .
Теперь прибавим эти уравнения и получим
Заметим, что . Следовательно,
. Рассмотрим оба варианта (х - 4у = 2 и х - 4у = -2), и для каждого варианта решим систему:
I вариант
II вариант:
Решений нету
Следовательно, у системы есть 2 решения - или
. Проверь сам, они подходят!
решение правильное, но в самом начале вы допустили небольшую ошибку(опечатку). Вы не складываете, а вычитаете из первого - второе, так как иначе вы не сможете упростить многочлен до куба разности. Правильная запись: x^3 - 64y^3 - 12x^2y + 48xy^2 = 8
Кстати, сейчас я заметил, что хотя вы и написали, что складываете уравнения, на деле в правой части у вас получается результат разности 56 и 48, значит все таки это опечатка и вы имели ввиду именно разность. Но знаки все же в получившемся уравнении лучше поменять.
Согласен
Похожие вопросы
Предмет: Немецкий язык,
автор: mikitinbogdan81
Предмет: Українська література,
автор: ssvalka4
Предмет: Оʻzbek tili,
автор: muslimabtscom
Предмет: Другие предметы,
автор: Аноним