Question

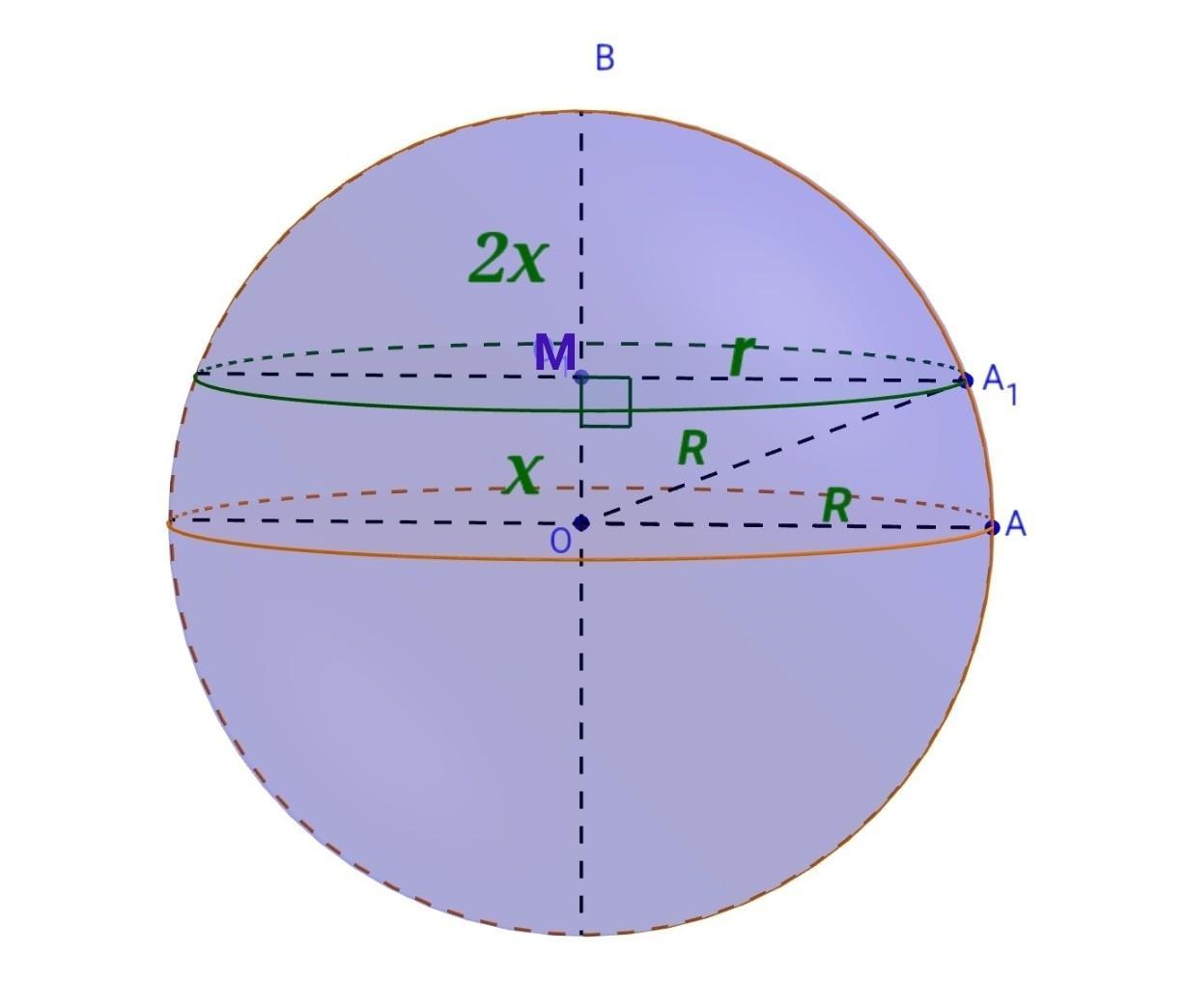
Радіус кулі поділено точкою М у відношенні 1 : 2, раху- ючи від центра кулі. Через точку М проведено переріз перпендикулярно до цього радіуса. Знайдіть відношення площі перерізу до площі великого круга кулі.


СРОЧНО ПОМОГИТЕ!!!!

Answer 1

Ответ:

Відношення площі перерізу до площі великого круга кулі дорівнює 8/9.

Объяснение:

УМОВА: Радіус кулі поділено точкою М у відношенні 1 : 2, рахуючи від центра кулі. Через точку М проведено переріз перпендикулярно до цього радіуса. Знайдіть відношення площі перерізу до площі великого круга кулі.

РОЗВ'ЯЗАННЯ

• Переріз кулі будь якою площиною завжди буде круг.
• Відстань від центра кулі до перерізу - перпендікуляр опущений з центра кулі до центра кругу, який є перерізом.

1) Маємо кулю з радіусом R = ОВ = OA = OA₁. Точка М∈ОВ, OM - відстань від центра кулі до перерізу.

ОМ : МВ = 1 : 2.

Круг з радіусом r = MA₁, MA₁⟂OM.

2) Нехай ОМ = х, а МВ = 2х, де х - коефіцієнт пропорційності.

Тоді R = OB = OM + MB = x + 2x = 3x

3) З прямокутного трикутника OMA₁(∠OMA₁=90°), в якому ОМ = х - катет, ОА₁ = 3х - гіпотенуза, за теоремою Піфагора знайдемо катет МА₁ = r - радіус круга - перерізу кулі площиною:

MA₁² = OA₁² - OM²

r² = MA₁² = (3x)² - x² = 9x² - x² = 8x²

4) Площа перерізу рівна:

S₁ = πr² = π • 8x²

5) Площа великого круга рівна:

S₂ = πR² = π • (3x)² = π • 9x²

6) Знайдемо відношення площин:

$\dfrac{S_1}{S_2} = \dfrac{\pi\cdot8 {x}^{2} }{\pi\cdot9 {x}^{2} } = \dfrac{8}{9}$

ВІДПОВІДЬ: 8/9

#SPJ1