Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Використовуючи метод інтегрування частинами, обчислити.
Приложения:

Ответы
Автор ответа:
1
Ответ:
Интегрирование по частям .
Приложения:
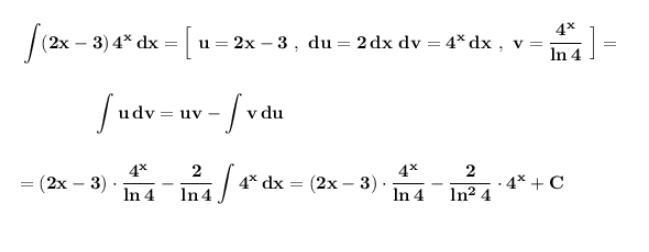
fctdgsygfdhngfxzgsac:
спасибо большое)
Похожие вопросы
Предмет: Литература,
автор: vojtukanastasia62
Предмет: Астрономия,
автор: vvcvhgbghj
Предмет: Обществознание,
автор: kiraporodko
Предмет: Математика,
автор: tanyaasmanova117
Предмет: Русский язык,
автор: zhanna81830810