даю 60 баллов Помогите пожалуйста с решением по математике
найти неопределённый интеграл
1) ∫(√x+2)^2 +3x/x^2 dx 2) ∫in^3 x+1/x dx
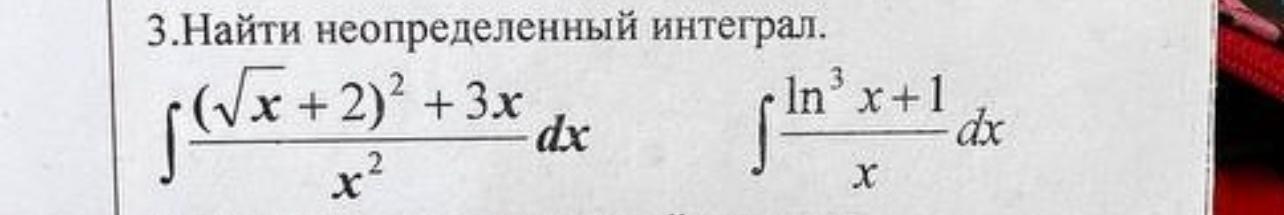

Ответы
1. ∫(√x+2)^2 +3x/x^2 dx
Рассмотрим первый интеграл:
∫(√x+2)^2 +3x/x^2 dx
Первый член можно разложить как:
(√x+2)^2 = x+4+2√x
Тогда интеграл примет вид:
∫(x+4+2√x) +3x/x^2 dx
Теперь можно интегрировать каждый член по отдельности:
∫x dx = x^2/2
∫4 dx = 4x
∫2√x dx = 2x^(3/2)/3
∫3x/x^2 dx = 3ln|x|
Тогда:
∫(√x+2)^2 +3x/x^2 dx
= x^2/2 + 4x + 2x^(3/2)/3 + 3ln|x| + C
= (3x^2 + 8x + 4x^(3/2) + 6ln|x|)/6 + C
2. ∫in^3 x+1/x dx
Рассмотрим второй интеграл:
∫in^3 x+1/x dx
Первый член можно разложить как:
in^3 x = x^(3/2) * inx
Тогда интеграл примет вид:
∫x^(3/2) * inx +1/x dx
Теперь можно интегрировать каждый член по отдельности:
∫x^(3/2) * inx dx = (2/3)x^(5/2) * inx + C
∫1/x dx = ln|x| + C
Тогда:
∫in^3 x+1/x dx
= (2/3)x^(5/2) * inx + ln|x| + C
Ответы:
∫(√x+2)^2 +3x/x^2 dx = (3x^2 + 8x + 4x^(3/2) + 6ln|x|)/6 + C
∫in^3 x+1/x dx = (2/3)x^(5/2) * inx + ln|x| + C