Предмет: Алгебра,
автор: Аноним
Даю 40 балов!!!!!!!Доведіть,що при будь-яких значених х різниця виразів набуває невід'ємних значень. Срочноооооооо
Приложения:
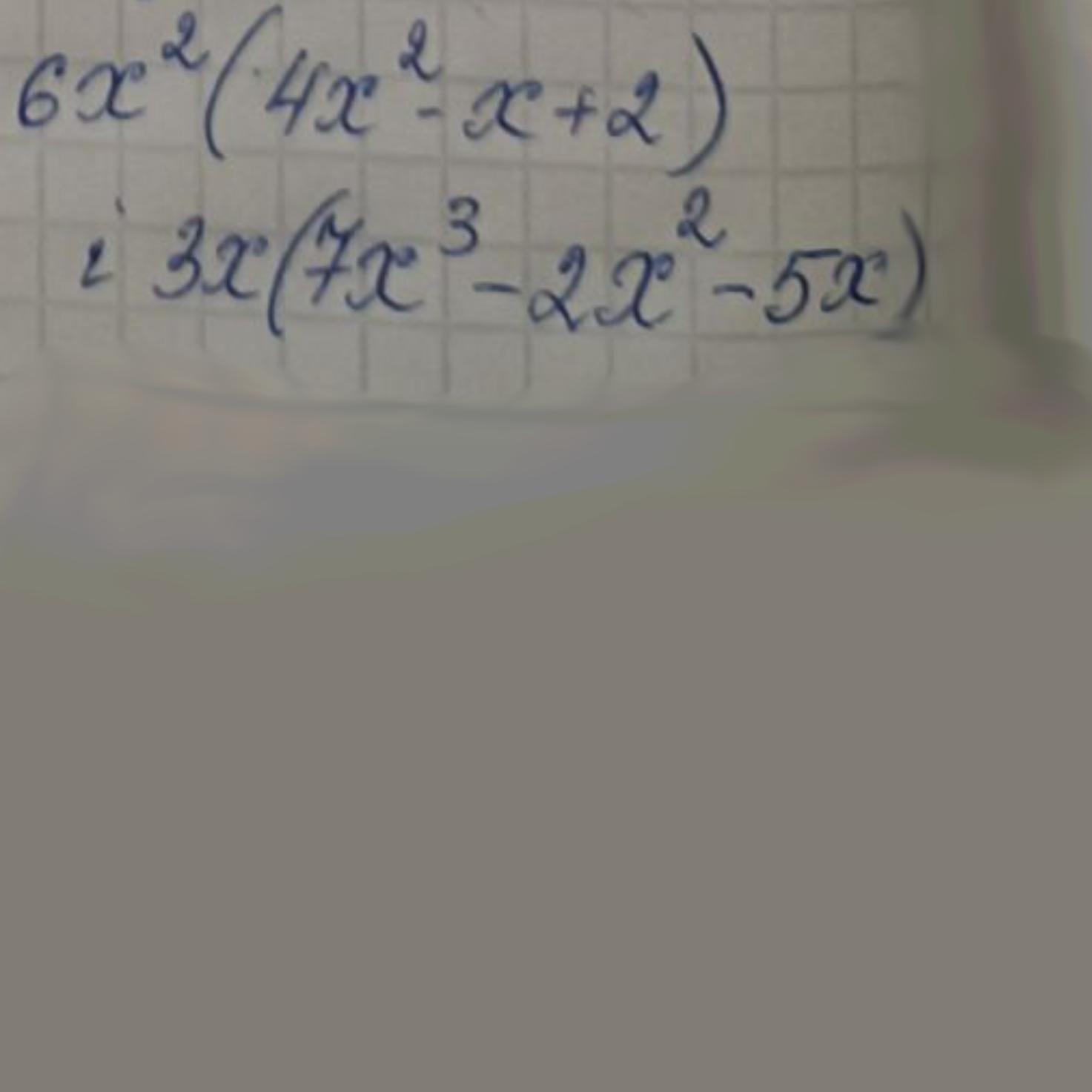
Ответы
Автор ответа:
0
Дискриминант меньше нуля , старший коэффициент больше нуля , значит 3x² + x + 27 > 0 при любых действительных значениях x .
Следовательно разность этих выражений ≥ 0 .
Похожие вопросы
Предмет: История,
автор: kirasbar1
Предмет: Химия,
автор: ola24061986
Предмет: Химия,
автор: baranovadd59
Предмет: Қазақ тiлi,
автор: Аноним