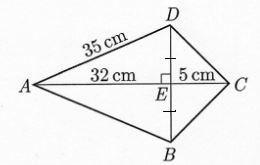
Вычислите периметр и площадь фигуры. Не забудьте доказать равенство треугольников.
Ответы
Ответ:
Площадь фигуры равна 37√201cm²
Периметр фигуры равен (70+2√226)cm
Объяснение:
∆АDE - прямоугольный треугольник.
Теорема Пифагора:
DE=√(AD²-AE²)=√(35²-32²)=
=√((35-32)(35+32))=
=√(3*67)=√201cm.
DE=BE=√201cm
DB=2*DE=2√201cm
S(ADCB)=½*AC*DE=
=½*37*2√201=37√201cm².
∆DEC - прямоугольный треугольник
Теорема Пифагора:
DC=√(DE²+EC²)=√((√201)²+5²)=
=√(201+25)=√226cm.
P=2*AD+2*DC=2*35+2*√226=
=70+2√226cm
___________
∆ADE=∆ABE, по первому признаку.
Доказательство:
DE=EB, по условию
∠DEA=∠BEA=90°, как смежные равные углы.
АЕ- общая сторона треугольников ∆АDE и ∆АВЕ.
∆АDE=∆ABE, по первому признаку.
Что и требовалось доказать.
____________
∆DEC=∆BEC, по первому признаку.
DE=EB, по условию.
∠DEC=∠BEC=90°
EC- общая сторона треугольников ∆DEC и ∆ВЕС.
∆DEC=∆BEC, по первому признаку.
Что и требовалось доказать.
________