Предмет: Алгебра,
автор: kanishevanatalia8
Обчислити інтеграл зверху 9п/3знизу0 sin2xdx
Ответы
Автор ответа:
0
Ответ:
Вычислить определённый интеграл . Применяем формулу Ньютона-Лейбница .
Приложения:
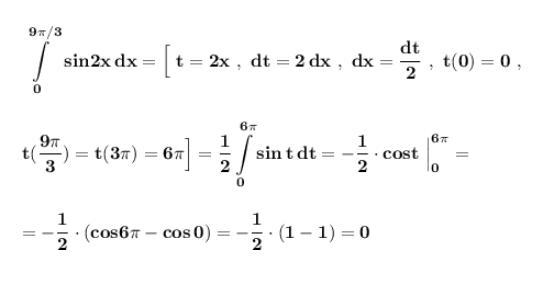
Похожие вопросы
Предмет: Математика,
автор: malozomovdanil999
Предмет: Английский язык,
автор: rimmar045
Предмет: Алгебра,
автор: sofysha10
Предмет: Русский язык,
автор: Momina22
Предмет: Геометрия,
автор: erasylikintai12765