II варіант №1 Градусна міра вписаного кута 80°. Знайдіть градусну міру дуги на яку спирається цей кут. №2 Менша сторона прямокутника BD 5см i утворюс з діагоналлю ZBDC 60° Знайти радіус описаного кола.
Ответы
Відповідь:
Пояснення:
Для першого випадку:
1. Градусна міра дуги, на яку спирається вписаний кут, дорівнює вдвічі більше, ніж величина самого кута, тобто 80° * 2 = 160°. Таким чином, градусна міра дуги становить 160°.
Для другого випадку:
2. Нехай точка O - центр описаного кола, яке вписане в прямокутник ABCD. Нехай AB=b, BC=a - сторони прямокутника. Так як діагональ ділить прямокутник навпіл, ми маємо, що \(DB^2=(\frac{a}{2})^2+(\frac{b}{2})^2\). Оскільки \(DB=5, \frac{a}{2}=\frac{5}{cos{30}}=\frac{5*2}{\sqrt{3}}\), тоді a=\( \frac{10}{\sqrt{3}}\). Аналогічно знаходимо b=\( \frac{10}{\sqrt{3}}\).
Таким чином, ОМ — радіус кола, яке описане навколо прямокутника ABCD, завдовжки "а".
Ответ:
Объяснение:
За т. про вписані та центральні кути.
Центральний кут, буде в двічі більший за вписаний : 80 × 2 = 160 градусів.
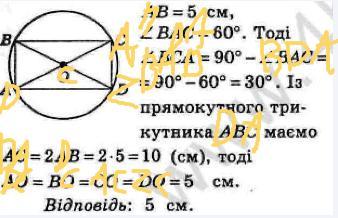
тороє на фото