Бобёр Вася выкинул из набора домино все костяшки с пустышками.
После этого у него осталась 21 костяшка. Каждая костяшка состоит
из двух половинок, на каждой половинке от 1 до 6 точек, при этом
все костяшки различны.
Вася попробовал выложить доминошки в ряд по следующему
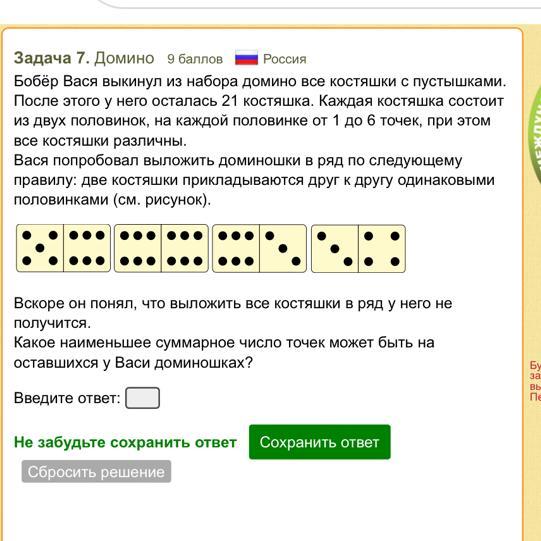
правилу: две костяшки прикладываются друг к другу одинаковыми
половинками (см. рисунок).
Вскоре он понял, что выложить все костяшки в ряд у него не
получится.
Какое наименьшее суммарное число точек может быть на
оставшихся у Васи доминошках?
Ответы
Ответ:
30
Объяснение:
Рассмотрим общее количество точек на всех доминошках: исходно у Васи было 21 костяшка.
Так как каждая костяшка состоит из двух половинок, и на каждой из них может быть от 1 до 6 точек, суммарное количество точек на всех доминошках равно 2×21=42
2×21=42 точки.
Теперь посмотрим на суммы точек на одинаковых половинках, которые могут соединяться между собой. Если они должны быть одинаковыми, то сумма точек на обеих половинках должна быть чётной. Поэтому, если у нас остались 42 точки, чтобы найти наименьшую сумму, которая не позволит выложить все доминошки, нужно найти наименьшее нечётное число, которое можно получить, вычитая чётные числа из 42.
Сумма чётных чисел от 2 до 6 равна
2+4+6=12
2+4+6=12. 42 минус 12 равно 30.
Таким образом, наименьшее суммарное число точек на оставшихся у Васи доминошках, которое не позволит выложить их все по правилам, равно 30.