Помогите пожалуйста решить задачу.
Нужно найти объем и полную поверхность пирамиды.
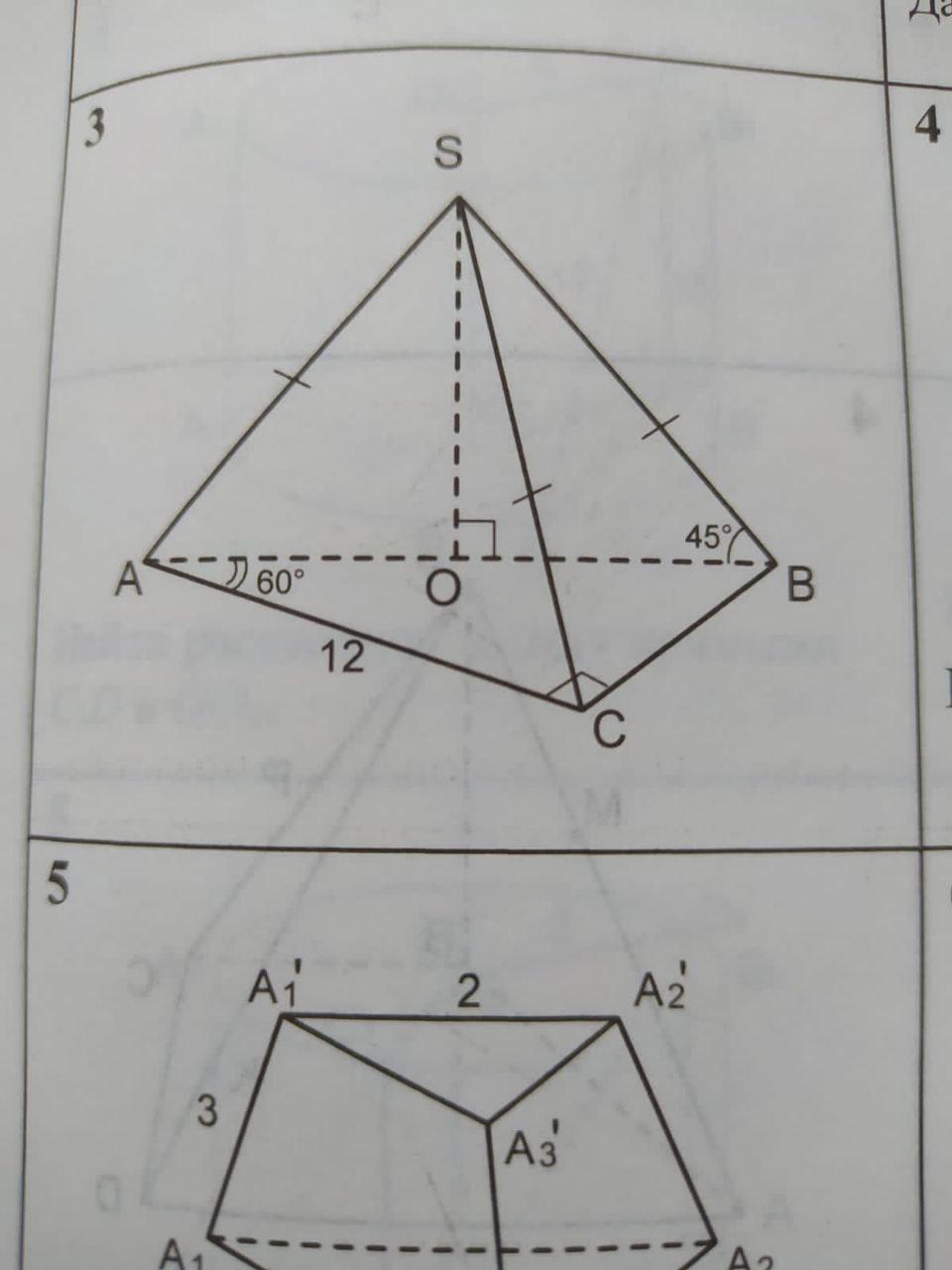
Ответы
Пошаговое объяснение:
Находим параметры прямоугольного треугольника основания пирамиды.
Сторона против угла 60 градусов равна: ВС = АС*tg 60° = 12*√3.
Гипотенуза АВ = АС/cos 60° = 12/(1/2) = 24.
Грань ASB вертикальна, медиана ОS является высотой пирамиды.
Площадь основания So = (1/2)AC*BC = (1/2)*12*12√3 = 72√3 ≈ 124,708 кв. ед.
Находим площади боковых граней по формуле Герона.
Треугольник ASC:
АS SС АС
16,97056275 16,97056275 12
Периметр Р = 45,9411255.
Полупериметр р = 22,97056275.
Площадь S = 95,247.
Треугольник CSB:
CS ВS BС
16,97056275 16,97056275 20,78460969
Периметр Р = 54,72573519.
Полупериметр р = 27,36286759.
Площадь S = 139,427.
Треугольник ASB:
АS ВS AB
16,97056275 16,97056275 24
Периметр Р = 57,9411255.
Полупериметр р = 28,97056.
Площадь S =144.
Площадь боковой поверхности равна:
Sбок = 95,247 + 139,427 + 144 = 378,674 кв. ед.
Полная площадь равна:
S = Sо + Sбок = 124,708 + 378,674 = 503,382 кв. ед.
Объём пирамиды равен:
V = (1/6)*So*H = (1/6)* 124,708*12 = 249,415 куб. ед.