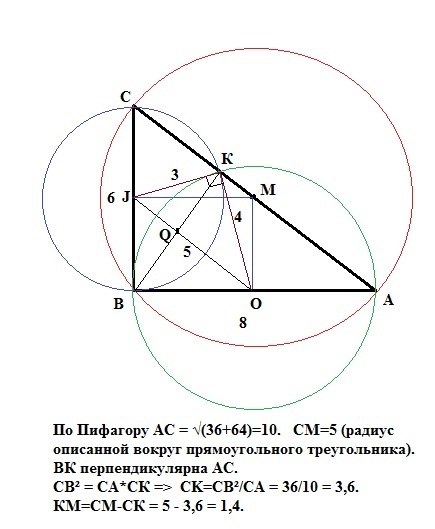
В прямоугольном треугольнике АВC на катетах АВ и ВС как на диаметрах построены окружности. Точка К принадлежит обеим окружностям и гипотенузе АС. Найдите расстояние от точки К до центра описанной около треугольника АВС окружности, если АВ=8 и ВС =6
Ответы
Сначала докажем, что действительно точка К пересечения двух окружностей, построенных на катетах ВС и ВА принадлежит гипотенузе АС. По Пифагору АС = √(36+64)=10 ед. Высота треугольника АВС, проведенная из прямого угла В, по ее свойству равна ВС*ВА/АС = 6*8/10 = 4,8 ед. ВК перпендикулярна OJ (отрезок, соединяющий центры пересекающихся окружностей), как общая хорда двух пересекающихся окружностей (свойство) и точкой Q делится пополам. OJ - средняя линия треугольника АВС (соединяет середины сторон АВ и ВС) => OJ=5. Тогда треугольник JKO - прямоугольный (Пифагоров - JK=3,OK=4,JK=5). QK- высота из прямого угла и QK = 3*4/5=2,4. Значит ВК = 2*2,4 = 4,8. Следовательно, отрезок ВК является высотой треугольника АВС и точка К лежит на гипотенузе АС, что и требовалось доказать.
Решение: по свойству высоты из прямого угла: СВ² = СА*СК => CK=CB²/CA = 36/10 = 3,6 ед. Точка М - центр описанной вокруг прямоугольного треугольника окружности - лежит на гипотенузе СА и СМ=СА:2 = 10:2 =5 ед (радиус окружности, описанной вокруг прямоугольного треугольника).
КМ=СМ-СК = 5 - 3,6 = 1,4 ед.