Предмет: Алгебра,
автор: sofiya3140
с рисунками пожалуйста
Приложения:
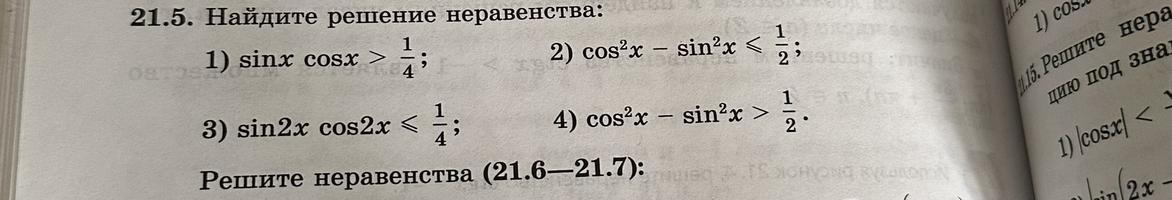
Ответы
Автор ответа:
0
Решение .
Применяем формулы двойных углов :
Приложения:
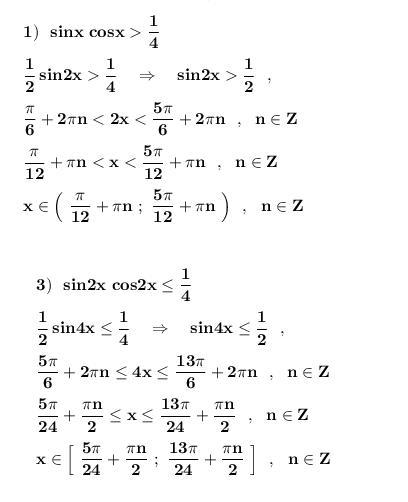
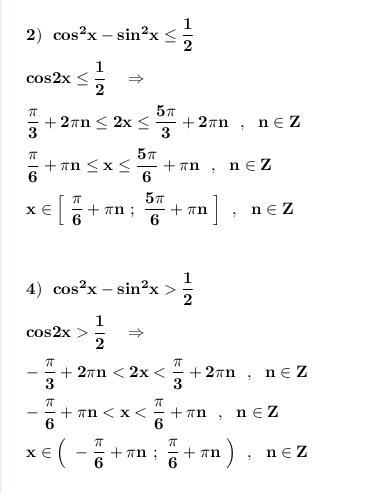
Похожие вопросы
Предмет: Литература,
автор: mifekapp
Предмет: Биология,
автор: abaizhakhan28
Предмет: Математика,
автор: a77963101
Предмет: Русский язык,
автор: ansaganmuzafar09
Предмет: Математика,
автор: usmanbekovmako