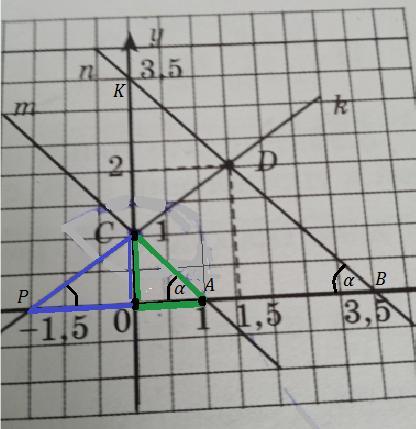
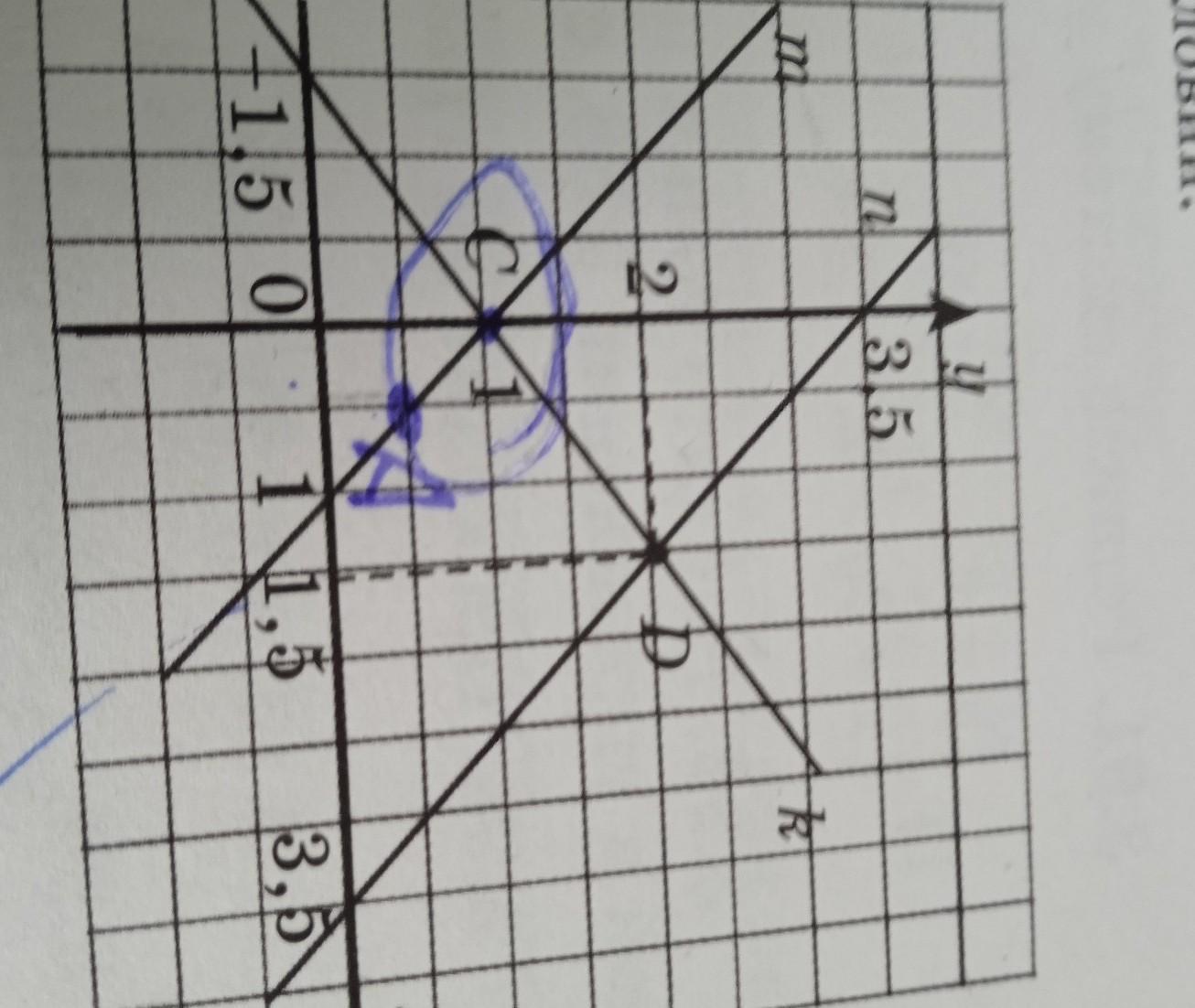
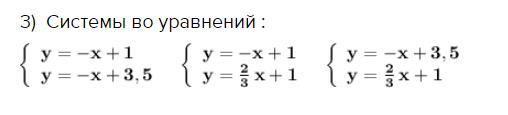3 1) По рисунку 3.30 напишите уравнения прямых м, п и к и запишите их в виде линейного уравнения. 2) Определите координаты точек С и D. 3) С помощью полученных трех линейных уравнений составьте попарно всевозмож- ные системы линейных уравнений. Среди них укажите системы, имеющие единствен- ное решение, и систему, не имеющую ре- n 35 шения. 4) Можно ли составить систему, имеющую бесконечно много решении, с помощью указанных уравнений? Чему равно коли- чество подобных систем, если можно соста- вить такую схему? (Целесообразно выполнить задания в группе.) 2 1/5 0 P
Ответы
Ответ:
Уравнение прямой с угловым коэффициентом k имеет вид :
y = kx + b , где b - ордината точки пересечения прямой с осью ОУ .
1) Прямая m пересекает ось ОУ в точке С( 0 : 1 ) , а ось ОХ в точке
А( 1 ; 0 ) . Исходя из этих данных можно записать уравнение прямой
m , проходящей через две точки .
Но можно найти из зелёного треугольника АОС угол α и определить тангенс этого угла : tgα = OC / OA = 1/1 = 1 ⇒ Значит угол α = 45° .
Тогда угол наклона прямой m к положительному направлению оси ОХ равен 180° - 45° = 135° и tg135° = -1 . Это будет угловым коэффициентом прямой m : k = -1 .
Тогда уравнение прямой m имеет вид : y = -x + 1 .
Как видим, прямая n параллельна прямой m , так как их угловые коэффициенты равны , tgα = OK/OB = 1 ⇒ k = -1 .
Ось ОУ прямая пересекает в точке К( 0 : 3,5 ) , поэтому b = 3,5 и уравнение прямой n : y = -x + 3,5 .
Найдём уравнение прямой k . Угловой коэффициент этой прямой можно найти из cинего треугольника ОСР .
k = tg∠ОРС = СО/ОР = 2/3 , пересекает ось ОУ прямая k в точке
C( 0 ; 1 ) , поэтому b = 1 . Уравнение k : y = 2x/3 + 1 .
2) C( 0 ; 1 ) , D( 1,5 ; 2 )
3) Cистемы линейных уравнений :
Единственное решение имеют 2 и 3 системы , так как прямые m , k и прямые n , k пересекаются в одной точке .
Система, не имеющая решений , - это 1 система , так как прямые m и n не пересекаются , они параллельны .
4) Составить систему, имеющую бесконечно много решений из таких трёх уравнений, как мы получили нельзя . Можно было бы написать уравнение одной и той же прямой дважды в системе , тогда она имела бы бесчисленное множество решений . Но можно было бы второе уравнение, чтобы оно не выглядело таким же, как и первое уравнение системы, записать так, чтобы его коэффициенты и свободный член были пропорциональны . Например,
Если менять коэффициент пропорциональности . то таких систем можно составить бесконечно много .