Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Вища математика. Інтеграли.
Приложения:
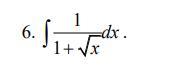
Ответы
Автор ответа:
1
Ответ:
в объяснении
Объяснение:
fctdgsygfdhngfxzgsac:
спасибо большое)
пожалуйста ))
Похожие вопросы
Предмет: Биология,
автор: darinamarmur071
Предмет: Химия,
автор: mularkarolina97
Предмет: Биология,
автор: papaetoprikolno
Предмет: Биология,
автор: khadishhhuuuuuuuha66
Предмет: Математика,
автор: mashakashokker