Предмет: Алгебра,
автор: qwiwie1819
Помогите пожалуйста!!!
Задание на фото
Вычислить интеграл
Приложения:
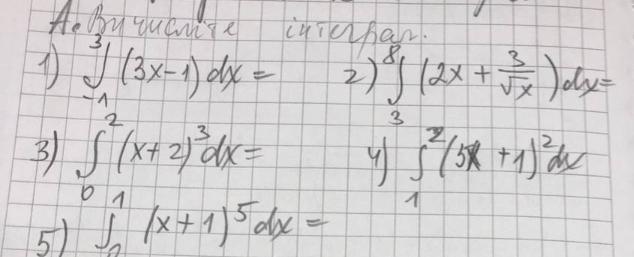
Ответы
Автор ответа:
2
Решение .
При вычислении определённых интегралов применяем формулу Ньютона-Лейбница .
Приложения:
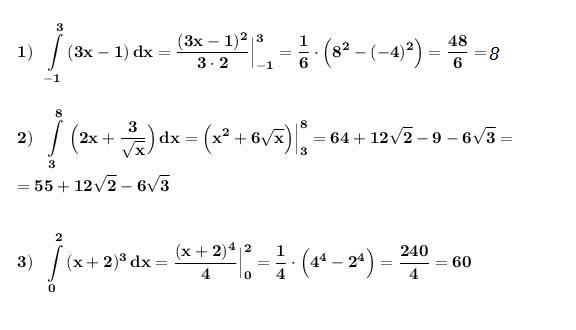
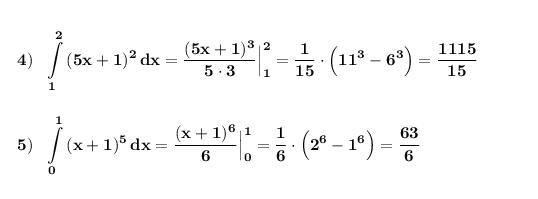
Похожие вопросы
Предмет: Литература,
автор: almas40
Предмет: Математика,
автор: ruslanbakirov1985
Предмет: Другие предметы,
автор: polinagolovachova20
Предмет: Литература,
автор: fafavaop
Предмет: Другие предметы,
автор: nazar200699