Question

Угол между биссектрисой и высотой, исходящих из вершины прямого угла, равен 24°. Найти меньший угол треугольника.

Answer 1

Дано:
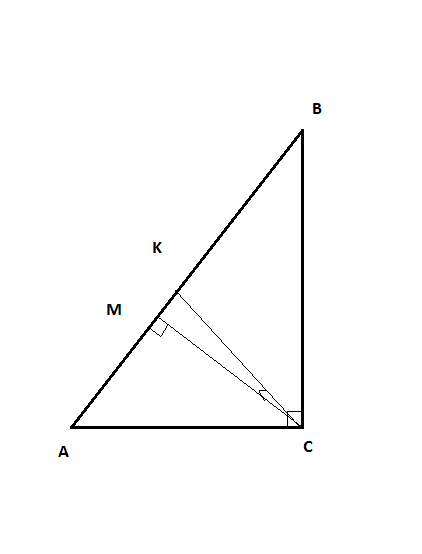
АВС - прямоугольный
<MCK = 24°
Найти: <B
1. После построения высоты СМ видим прямоугольный треугольник АМС, <АМС = 90°. Поскольку биссектриса СК делит прямой угол С пополам, то
<АСК = 90 : 2 = 45°.
Зная угол МСК и АСК, находим угол АСМ:
<АСМ = <ACK - <MCK = 45 - 24 = 21°
2. Находим в треугольнике АМС последний неизвестный угол А, зная, что сумма углов треугольника равна 180°:
< А = 180 - <АМС - <АСМ = 180 - 90 - 21 = 69°
3. Находим неизвестный угол В в треугольнике АВС, зная его углы С и А:
<В = 180 - 90 - 69 = 21°