Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Обчислити інтеграли методом заміни змінних.
Приложения:
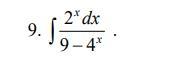
Ответы
Автор ответа:
1
Ответ:
Метод замены переменной .
Применяем формулу ,
Приложения:
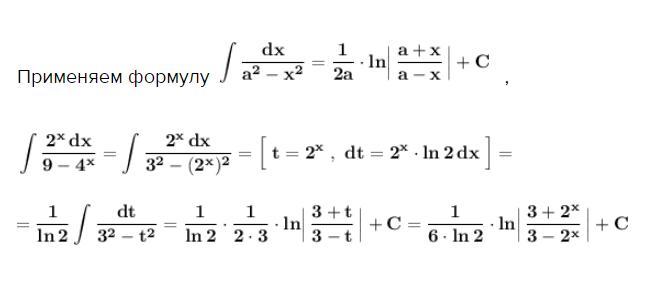
fctdgsygfdhngfxzgsac:
спасибо большое)
Похожие вопросы
Предмет: Математика,
автор: dendi12345d
Предмет: Английский язык,
автор: kenzhebek67
Предмет: Музыка,
автор: vikanagornay13
Предмет: Қазақ тiлi,
автор: diasbospan
Предмет: Русский язык,
автор: mazhar84