Question

Помогите с геометрией, даю много баллов↓
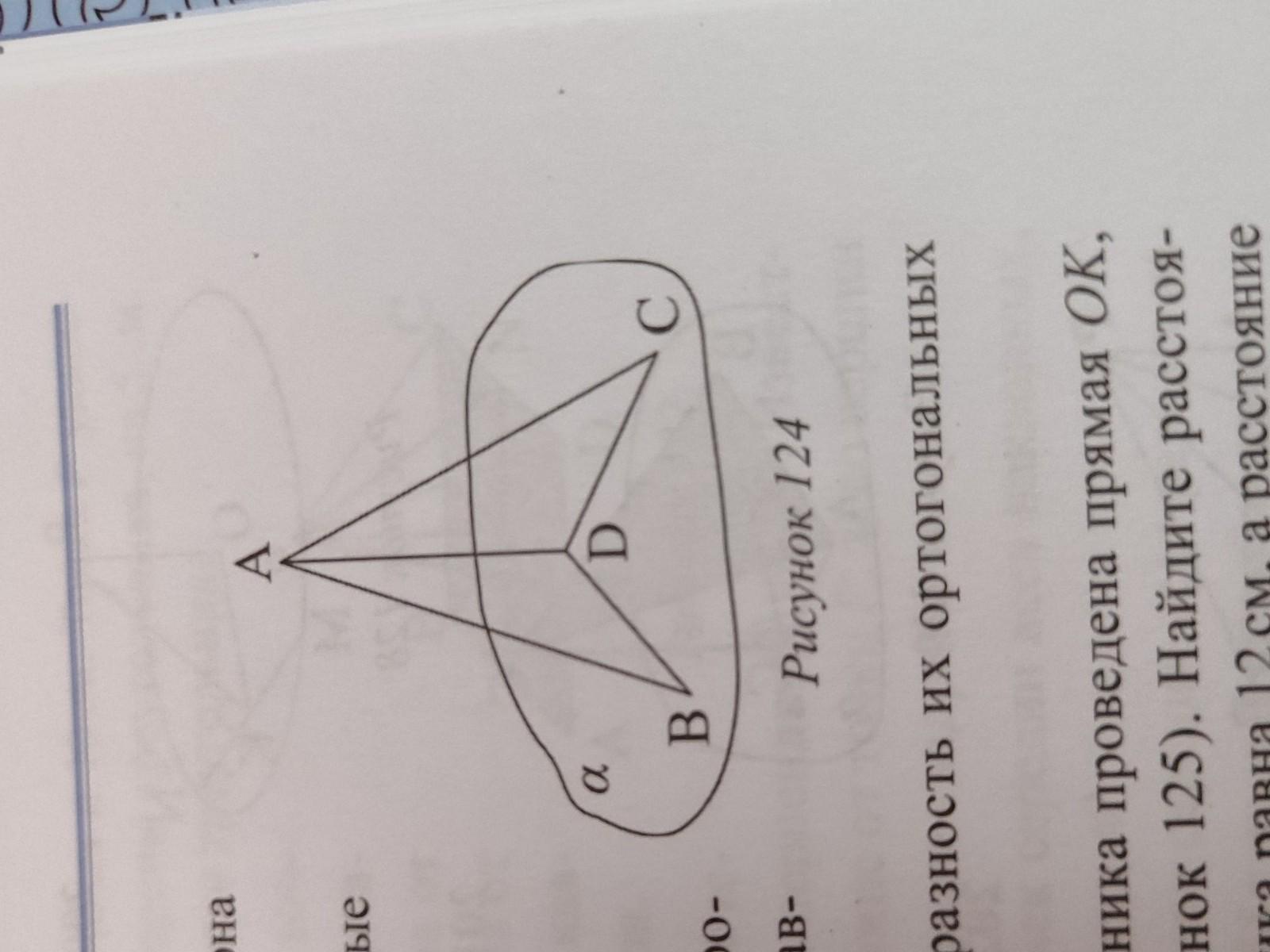
на рисунке 124 прямая AD перпендикулярна плоскости a. Найдите длину отрезка AD, если: AB:AC=10:17, а ортогональные проекции этих наклонных на плоскость a равны 12 см и 30 см
​

Answer 1

Ответ:

AD = 16 см

Объяснение:

УМОВА: на рисунке 124 прямая AD перпендикулярна плоскости α. Найдите длину отрезка AD, если: AB:AC=10:17, а ортогональные проекции этих наклонных на плоскость α равны 12 см и 30 см.

РЕШЕНИЕ:

AD⟂α, AB и AC - наклонные к плоскости α. BD - проекция АВ, DC - проекция АС.

Пусть АВ = 10х, АС = 17х, де х - коэффициент пропорциональности.

Так как АВ < АС, то и BD < DC. Тогда BD = 12 см, DC = 30 см.

Найдём AD.

1) В прямоугольном треугольнике ADC (∠D=90°) по теореме Пифагора найдём катет AD.

AD² = AB² - BD²

AD² = (10x)² - 12² = 100x² - 144

2) В прямоугольном треугольнике ACD(∠D=90°) по теореме Пифагора найдём катет АD.

AD² = AC² - DC²

AD² = (17x)² - 30² = 289x² - 900.

3) Решим уравнение:

100х² - 144 = 289х² - 900

189х² = 756

х² = 756 : 189

х² = 4

х = 2 (Так как х > 0 по условию).

4) AD² = 100 • 2² - 144 = 400 - 144 = 256

AD = √256 = 16 см

ОТВЕТ: 16 см

#SPJ1