Предмет: Алгебра,
автор: hshsznzn75
{5√x²-3y-1+√x+6y=19
{3√x²-3y-1=1+2√x+64
pomóżcie mi rozwiązać układ równań
помогите решить систему уравнений
Приложения:
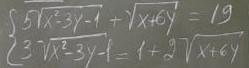
Ivan19074:
корень х квадрат это как?
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Введём обозначения и
. Тогда получим
, откуда
, а
.
Подставив эти данные, получим новую систему, которая тоже довольно легко решается:
Рассмотрим вариант №1:
Рассмотрим вариант №2:
Итак, всего есть 2 решения: .
Проверяй!
Похожие вопросы
Предмет: Физика,
автор: danikkiselev79
Предмет: История,
автор: aiiishakanatovna2011
Предмет: Химия,
автор: Аноним
Предмет: Алгебра,
автор: anImE090
Предмет: Литература,
автор: amirsafin1812