Предмет: Алгебра,
автор: mishabez152
довести рівність срочно допоможіть!!!!!!
Приложения:
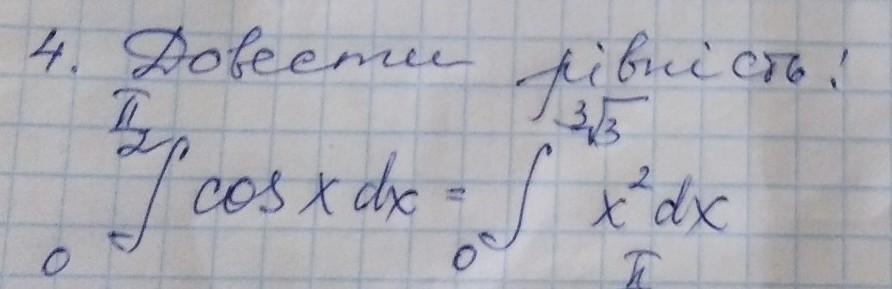
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Похожие вопросы
Предмет: Физика,
автор: nurajmoskva
Предмет: Математика,
автор: dilfuzareimbergenova
Предмет: Математика,
автор: elmirasabitova340
Предмет: География,
автор: irinanet444
Предмет: Английский язык,
автор: aloevolkova