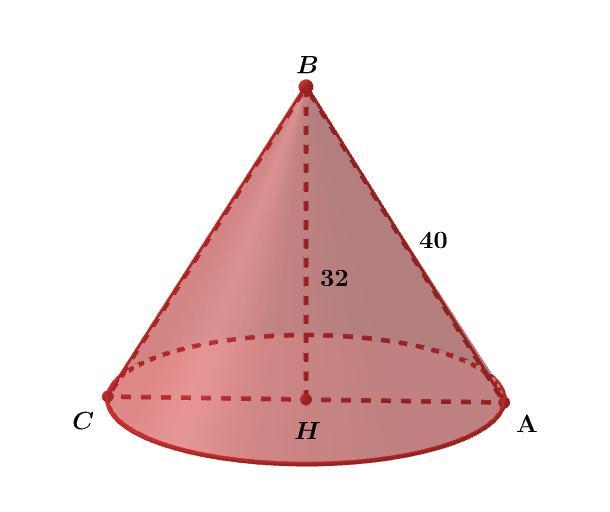
Высота конуса равна 32, а длина образующей – 40. Найдите площадь осевого сечения этого конуса.
Ответы
Ответ:
Площадь осевого сечения данного конуса равняется 768 квадратных единиц.
Пошаговое объяснение:
Дано:
Конус;
AB и CB - образующие;
AB = CB = 40;
BH - высота;
BH = 32.
Чертёж:
См. во вложении.
Найти:
S осевого сечения - ?
Решение:
Осевое сечение - это сечение конуса плоскостью, проходящей через его ось.
Осевым сечением конуса является равнобедренный треугольник, основанием которого является диаметр окружности, а боковые стороны являются образующими данного конуса.
В нашем случае, осевым сечением конуса будет являться равнобедренный треугольник ABC.
Высота конуса ВH является высотой осевого сечения (треугольника).
1) Рассмотрим прямоугольный треугольник ABH.
По теореме Пифагора (в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов):
AB² = AH² + BH²;
Из условия нам известно, что высота BH = 32, а длина образующей AB = 40.
Значит:
40² = AH² + 32²;
AH² = 40² - 32² = (40 - 32) (40 + 32) = 8 × 72 = 576;
AH = √576 = 24.
2) В равнобедренном треугольнике высота также является медианой.
Значит:
AH = CH;
AC = AH + CH = AH + AH = 2AH;
AC = 2 × 24 = 48.
3) Площадь треугольника равна полупроизведению основания и высоты.
То есть:
S = × AC × BH;
--------------
Удачи! :)
--------------
#SPJ1