Предмет: Геометрия,
автор: efimenkozena674
Допоможіть будь ласка з цією задачею.
Приложения:

Ответы
Автор ответа:
4
Ответ:
Площа бічної поверхні піраміди дорівнює (18√3+36√6)см²
Объяснение:
S(∆ABC)=AB²√3/4; →
AB=√(4*S(∆ABC)/√3)=
=√(4*36√3/√3)=2*6=12см.
∆НКВ- прямокутний трикутник, з кутами 30°;60°;90°
КВ- катет проти кута 30°
КВ=НВ/2=6/2=3см
НК=КВ√3=3√3см
∆МНК-прямокутний, рівнобедрений трикутник.
Кути при основі рівні по 45°; ∠МКН=∠НМК=45°
НК=МН=3√3см.
∆MKH- прямокутний трикутник
Теорема Піфагора:
МК=√(МН²+НК²)=√((3√3)²+(3√3)²)=
=3√6см
S(∆MBC)=½*MK*BC=½*3√6*12=
=18√6см²
S(∆MAC)=18√6см²
S(∆MAB)=½*AB*MH=½*12*3√3
=18√3см²
Sб=2*S(∆MBC)+S(∆MAB)=
=18√3+2*18√6=18√3+36√6см²
Приложения:
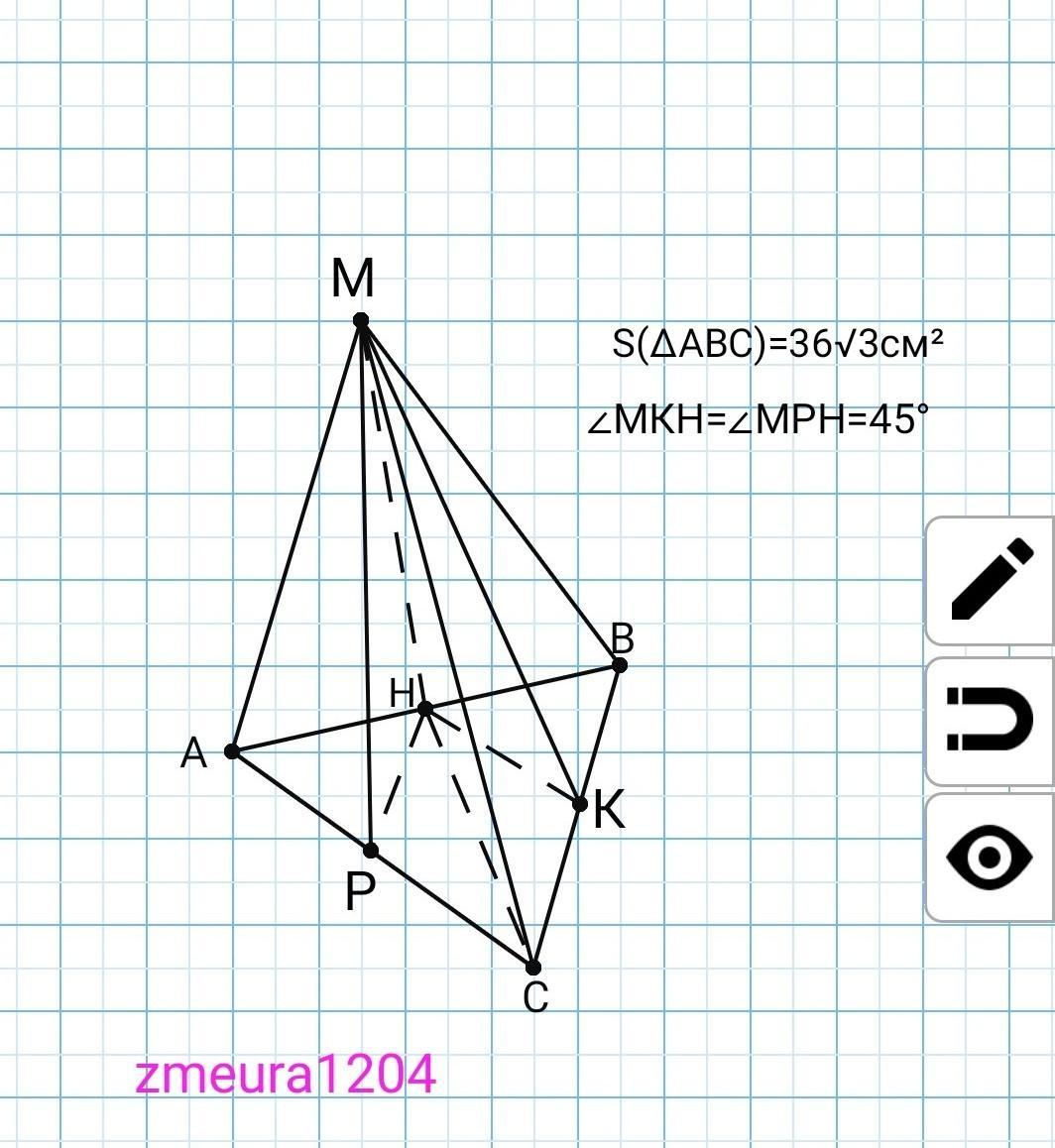
zmeura1204:
Ой, це неправильно.
Вибачте, а як буде правильно?
Я можу додати балів
Дуже вам дякую за відповідь
Зараз буду переписувати.
Велике вам дякую
Ось так, дві грані нахилені. А я в перший раз одну нахилила.
Велике вам дякую!!!!!
добро дня, zmeura1204, дуже прошу вас допомогти з останнім моїм запитанням по геометрії
дуже прошу
Похожие вопросы
Предмет: История,
автор: rostikyacenko2
Предмет: Английский язык,
автор: lenamironenko46
Предмет: Физика,
автор: dgonideppop
Предмет: Математика,
автор: anastasiya200923
Предмет: Алгебра,
автор: msgulyu