Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Користуючись методом розкладу, обчислити інтеграли.
Приложения:
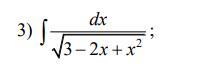
Ответы
Автор ответа:
1
Ответ:
Выделяем полный квадрат из квадратного трёхчлена :
Можно для простоты понимания , какую табличную формулу применить , заменить на t разность х-1 : t = x - 1 , тогда
.
Получим окончательный ответ :
Приложения:

fctdgsygfdhngfxzgsac:
спасибо большое)
Похожие вопросы
Предмет: Литература,
автор: alexandrperesynko201
Предмет: Английский язык,
автор: Valeron2007
Предмет: Литература,
автор: haliullinaskar37
Предмет: Химия,
автор: tsariukschool