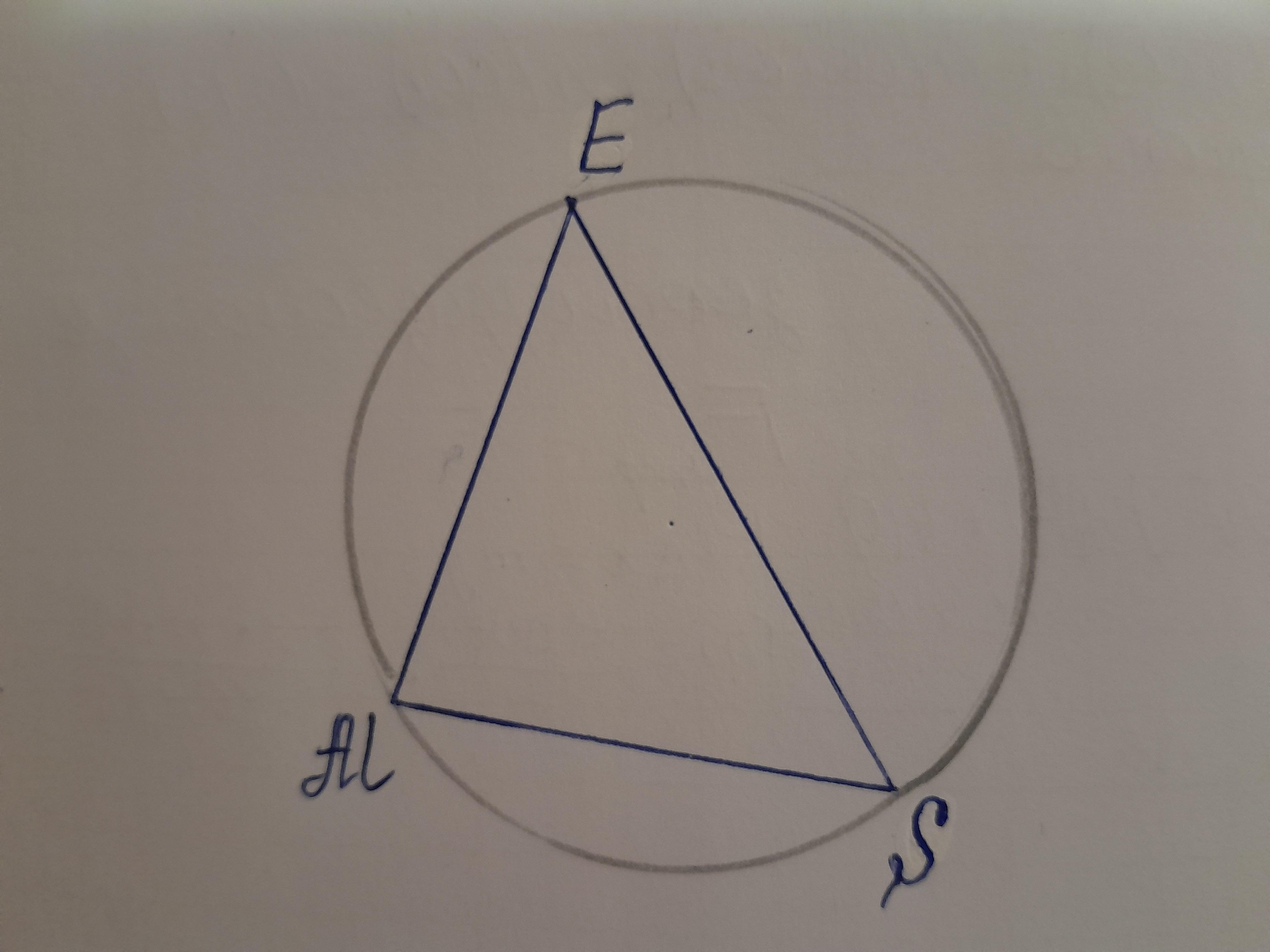
Вершини трикутника MSE дiлять коло у відношенні 3: 8:4. Знайдіть кути цього трикутника. З розв'язанням. Допоможіть будь ласка зробити
Ответы
Ответ:
Объяснение:Для знаходження кутів трикутника MSE спочатку знайдемо кути, утворені вершинами трикутника на колі.
Відомо, що кут, утворений хордою та дотичною до кола у точці дотику, дорівнює половині кута, що відповідає цьому дотичному відрізку на колі.
Отже, кути, утворені вершинами трикутника на колі, будуть дорівнювати 3x, 8x та 4x, де x - це половина кута, що відповідає цьому відрізку на колі.
Таким чином, сума кутів трикутника MSE дорівнює 180 градусів. Тобто:
3x + 8x + 4x = 180
15x = 180
x = 12
Тепер знаходимо значення кутів:
Кут M = 3x = 3 * 12 = 36 градусів
Кут S = 8x = 8 * 12 = 96 градусів
Кут E = 4x = 4 * 12 = 48 градусів
Отже, кути трикутника MSE дорівнюють 36°, 96° та 48°.
Ответ:
Объяснение:
Дано:
MS = 3х
ME = 8x
ES = 4x
Найти: ∠∆ - ?
Сума ччастин: 3 + 8 + 4 = 15
Знайдемо частинм кола:
MS = (360/15) * 3 = 72°
ME = (360/15) * 8 = 192°
ES = (360/15) * 4 = 96°
Кути трикутника вписані, отже вони вдвічі менше дуг на які спираються:
∠Е = MS / 2 = 72/ 2 = 36°
∠S = ME / 2 = 192 / 2 = 96°
∠М = ES / 2 = 96 / 2 = 48°