Предмет: Математика,
автор: azirools
(a ^ 5 - a)/(a ^ 5 - a ^ 9)
Приложения:
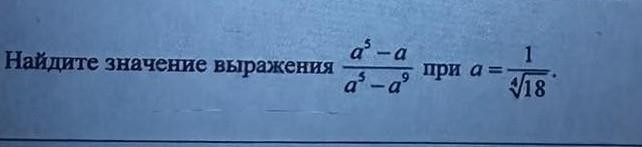
Ответы
Автор ответа:
0
Ответ:
-18
Пошаговое объяснение:
ОДЗ:
Эти условия выполняются, следовательно это выражение имеет значение.
Вынесем за скобки общие делители числителя и знаменателя, а затем сократим:
Следовательно, .
То есть, значение выражения равно -18.
Похожие вопросы
Предмет: Биология,
автор: karina2212019
Предмет: Химия,
автор: alekseyalexsandrov
Предмет: Химия,
автор: danilkudiy69
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: Аноним