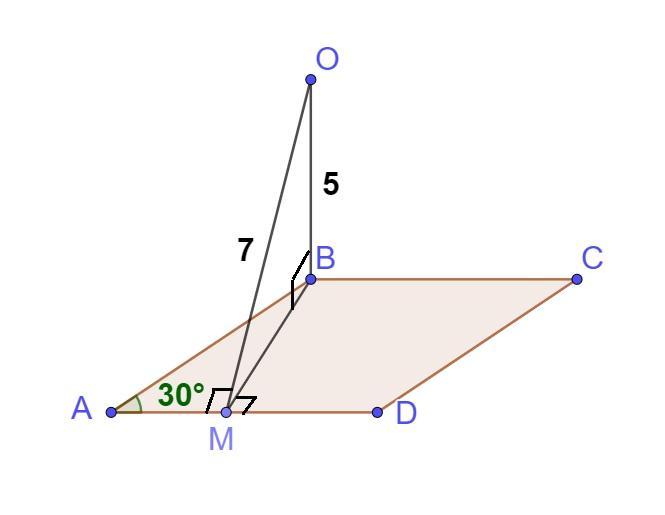
Острый угол ABCD равен 30°. Через вершину B тупого угла проведён отрезок OB, перпендикулярный плоскости ромба ABCD. Найдите площадь ромба ABCD, если OB=5 и расстояние от точки O до стороны AD ромба равно 7.
Ответы
Ответ:
Площадь ромба равна 48 кв. ед.
Объяснение:
Острый угол ABCD равен 30°. Через вершину B тупого угла проведён отрезок OB, перпендикулярный плоскости ромба ABCD. Найдите площадь ромба ABCD, если OB=5 и расстояние от точки O до стороны AD ромба равно 7.
1. ОВ⊥(ABC) , поэтому (по свойству) ОВ перпендикулярна каждой прямой, принадлежащей плоскости АВС (ромба ABCD).
Расстояние от точки О до стороны АD ромба ABCD - перпендикуляр опущенный из точки О на прямую АD , т.е. ОM⊥АD .
ОМ = 7.
Проведем отрезок ВM .
Поскольку ОВ – перпендикуляр к плоскости ABC , то ОM – наклонная (точка M – основание наклонной), а отрезок ВM – проекция наклонной на плоскость ABC . Так как ОM⊥АD , то по теореме «о трех перпендикулярах» (если отрезок, проведенный через основание наклонной перпендикулярен к наклонной, то он перпендикулярен и к ее проекции, и наоборот), ВM⊥АD .
Отсюда следует, что ВM – высота ромба ABCD, проведенная к стороне АD.
2. Рассмотрим прямоугольный ΔОВМ(∠В=90°).
Гипотенуза ОМ = 7, катет ОВ = 5. По теореме Пифагора найдём катет ВМ.
ВМ² = ОМ² - ОВ²
ВМ² = 7² - 5² = 49 - 25 = 24
ВМ = 2√6
3. Рассмотрим прямоугольный ΔАВМ (∠М=90°).
Катет ВМ лежит напротив ∠А = 30°, а следовательно (по свойству), равен половине гипотенузы АВ.
Таким образом:
АВ = 2 · ВМ = 2 · 2√6 = 4√6.
4. Так как у ромба все стороны равны, то AD = АВ = 4√6.
5. Площадь ромба найдём как произведение стороны на высоту, проведенную к этой стороне.
S(ABCD) = AD · BM
S(ABCD) = 4√6 · 2√6 = 48 (кв.ед)
Ответ: 48 кв. ед.
#SPJ1