Предмет: Алгебра,
автор: katyule4ka
lim стремится к 5 (sin πx/2) в степени 1/(x-1))
Приложения:
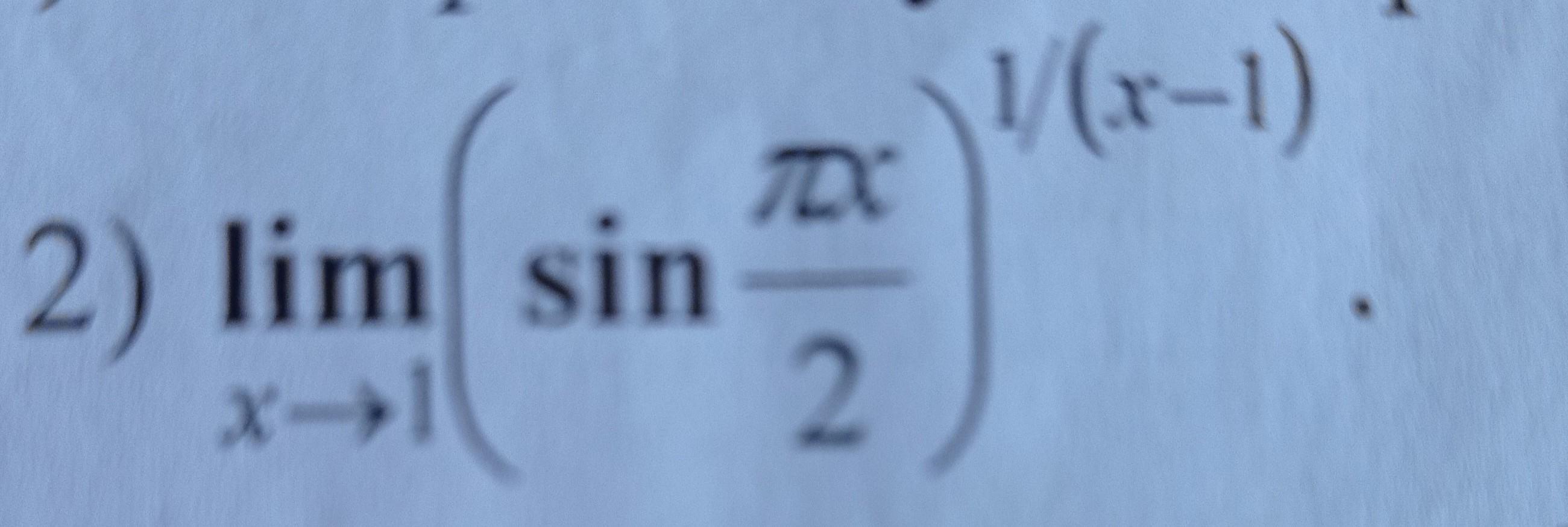
Ответы
Автор ответа:
2
Решение .
Вычислить предел . Применяем 2 замечательный предел .
Вычислим отдельно предел в показателе степени . Если можно по условию, то проще применить к вычислению этого предела правило Лопиталя .
.
Приложения:

Похожие вопросы
Предмет: Биология,
автор: sigmaUkr
Предмет: История,
автор: artem6996rud
Предмет: Биология,
автор: fernospolina
Предмет: Математика,
автор: Аноним
Предмет: Музыка,
автор: hamamatsuharajukugir